title: libigl Tutorial
author: Alec Jacobson, Daniele Pannozo and others
date: 20 June 2014
css: style.css
html header:   <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
<link rel="stylesheet" href="http://yandex.st/highlightjs/7.3/styles/default.min.css">
<script src="http://yandex.st/highlightjs/7.3/highlight.min.js"></script>
<script>hljs.initHighlightingOnLoad();</script>

# Introduction
Libigl is an open source C++ library for geometry processing research and
development.
Dropping the heavy data structures of tradition geometry libraries, libigl is
a simple header-only library of encapsulated functions. 
%
This combines the rapid prototyping familiar to \textsc{Matlab} or
\textsc{Python} programmers
with the performance and versatility of C++.
%
The tutorial is a self-contained, hands-on introduction to \libigl. 
%
Via live coding and interactive examples, we demonstrate how to accomplish
various common geometry processing tasks such as computation of differential
quantities and operators, real-time deformation, global parametrization,
numerical optimization and mesh repair.
%
Accompanying lecture notes contain further details and cross-platform example
applications for each topic.
\end{abstract}

# Index

* **100_FileIO**: Example of reading/writing mesh files
* **101_Serialization**: Example of using the XML serialization framework
* **102_DrawMesh**: Example of plotting a mesh
* [202 Gaussian Curvature](#gaus)
* [203 Curvature Directions](#curv)
* [204 Gradient](#grad)

# Compilation Instructions

All examples depends on glfw, glew and anttweakbar. A copy
of the sourcecode of each library is provided together with libigl
and they can be precompiled using:

**Alec: Is this just compiling the dependencies? Then perhaps rename `compile_dependencies_*`**

    sh compile_macosx.sh (MACOSX)
    sh compile_linux.sh (LINUX)
    compile_windows.bat (Visual Studio 2012)

Every example can be compiled by using the cmake file provided in its folder.
On Linux and MacOSX, you can use the provided bash script:

    sh ../compile_example.sh

## (Optional: compilation with libigl as static library)

By default, libigl is a _headers only_ library, thus it does not require
compilation. However, one can precompile libigl as a statically linked library.
See `../README.md` in the main directory for compilations instructions to
produce `libigl.a` and other libraries. Once compiled, these examples can be
compiled using the `CMAKE` flag `-DLIBIGL_USE_STATIC_LIBRARY=ON`:

    ../compile_example.sh -DLIBIGL_USE_STATIC_LIBRARY=ON

# Chapter 2: Discrete Geometric Quantities and Operators
This chapter illustrates a few discrete quantities that libigl can compute on a
mesh. This also provides an introduction to basic drawing and coloring routines
in our example viewer. Finally, we construct popular discrete differential
geometry operators.

## <a id=gaus></a> Gaussian Curvature
Gaussian curvature on a continuous surface is defined as the product of the
principal curvatures:

 $k_G = k_1 k_2.$

As an _intrinsic_ measure, it depends on the metric and
not the surface's embedding.

Intuitively, Gaussian curvature tells how locally spherical or _elliptic_ the
surface is ( $k_G>0$ ), how locally saddle-shaped or _hyperbolic_ the surface
is ( $k_G<0$ ), or how locally cylindrical or _parabolic_ ( $k_G=0$ ) the
surface is.

In the discrete setting, one definition for a ``discrete Gaussian curvature''
on a triangle mesh is via a vertex's _angular deficit_:

 $k_G(v_i) = 2π - \sum\limits_{j\in N(i)}θ_{ij},$

where $N(i)$ are the triangles incident on vertex $i$ and $θ_{ij}$ is the angle
at vertex $i$ in triangle $j$ [][#meyer_2003].

Just like the continuous analog, our discrete Gaussian curvature reveals
elliptic, hyperbolic and parabolic vertices on the domain.

![The `GaussianCurvature` example computes discrete Gaussian curvature and visualizes it in
pseudocolor.](images/bumpy-gaussian-curvature.jpg)

## <a id=curv></a> Curvature Directions
The two principal curvatures $(k_1,k_2)$ at a point on a surface measure how much the
surface bends in different directions. The directions of maximum and minimum
(signed) bending are call principal directions and are always
orthogonal.

Mean curvature is defined simply as the average of principal curvatures:

 $H = \frac{1}{2}(k_1 + k_2).$ 

One way to extract mean curvature is by examining the Laplace-Beltrami operator
applied to the surface positions. The result is a so-called mean-curvature
normal:

  $-\Delta \mathbf{x} = H \mathbf{n}.$ 

It is easy to compute this on a discrete triangle mesh in libigl using the cotangent
Laplace-Beltrami operator [][#meyer_2003].

```cpp
#include <igl/cotmatrix.h>
#include <igl/massmatrix.h>
#include <igl/invert_diag.h>
...
MatrixXd HN;
SparseMatrix<double> L,M,Minv;
igl::cotmatrix(V,F,L);
igl::massmatrix(V,F,igl::MASSMATRIX_VORONOI,M);
igl::invert_diag(M,Minv);
HN = -Minv*(L*V);
H = (HN.rowwise().squaredNorm()).array().sqrt();
```

Combined with the angle defect definition of discrete Gaussian curvature, one
can define principal curvatures and use least squares fitting to find
directions [][#meyer_2003].

Alternatively, a robust method for determining principal curvatures is via
quadric fitting [][#pannozo_2010]. In the neighborhood
around every vertex, a best-fit quadric is found and principal curvature values
and directions are sampled from this quadric. With these in tow, one can
compute mean curvature and Gaussian curvature as sums and products
respectively.

![The `CurvatureDirections` example computes principal curvatures via quadric
fitting and visualizes mean curvature in pseudocolor and principal directions
with a cross field.](images/fertility-principal-curvature.jpg)

This is an example of syntax highlighted code:

```cpp
#include <foo.html>
int main(int argc, char * argv[])
{
  return 0;
}
```

## <a id=grad></a> Gradient
Scalar functions on a surface can be discretized as a piecewise linear function
with values defined at each mesh vertex:

 $f(\mathbf{x}) \approx \sum\limits_{i=0}^n \phi_i(\mathbf{x})\, f_i,$

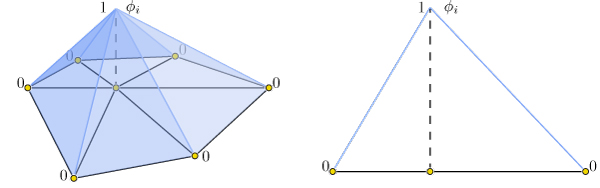
where $\phi_i$ is a piecewise linear hat function defined by the mesh so that
for each triangle $\phi_i$ is _the_ linear function which is one only at
vertex $i$ and zero at the other corners.

![Hat function $\phi_i$ is one at vertex $i$, zero at all other vertices, and
linear on incident triangles.](images/hat-function.jpg)

Thus gradients of such piecewise linear functions are simply sums of gradients
of the hat functions:

 $\nabla f(\mathbf{x}) \approx 
 \nabla \sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i = 
 \sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i.$

This reveals that the gradient is a linear function of the vector of $f_i$
values. Because $\phi_i$ are linear in each triangle their gradient are
_constant_ in each triangle. Thus our discrete gradient operator can be written
as a matrix multiplication taking vertex values to triangle values:

 $\nabla f \approx \mathbf{G}\,\mathbf{f},$

where $\mathbf{f}$ is $n\times 1$ and $\mathbf{G}$ is an $m\times n$ sparse
matrix. This matrix $\mathbf{G}$ can be derived geometrically, e.g.
[ch. 2][#jacobson_thesis_2013].
Libigl's `gradMat`**Alec: check name** function computes $\mathbf{G}$ for
triangle and tetrahedral meshes:

![The `Gradient` example computes gradients of an input function on a mesh and
visualizes the vector field.](images/cheburashka-gradient.jpg)

[#meyer_2003]: Mark Meyer and Mathieu Desbrun and Peter Schröder and Alan H.  Barr,
"Discrete Differential-Geometry Operators for Triangulated
2-Manifolds," 2003.
[#pannozo_2010]: Daniele Pannozo, Enrico Puppo, Luigi Rocca,
"Efficient Multi-scale Curvature and Crease Estimation," 2010.
[#jacobson_thesis_2013]: Alec Jacobson,
_Algorithms and Interfaces for Real-Time Deformation of 2D and 3D Shapes_,
2013.