title: libigl Tutorial
author: Alec Jacobson, Daniele Pannozo and others
date: 20 June 2014
css: style.css
html header:
# Introduction
Libigl is an open source C++ library for geometry processing research and
development. Dropping the heavy data structures of tradition geometry
libraries, libigl is a simple header-only library of encapsulated functions.
This combines the rapid prototyping familiar to Matlab or Python programmers
with the performance and versatility of C++. The tutorial is a self-contained,
hands-on introduction to libigl. Via live coding and interactive examples, we
demonstrate how to accomplish various common geometry processing tasks such as
computation of differential quantities and operators, real-time deformation,
global parametrization, numerical optimization and mesh repair. Each section
of these lecture notes links to a cross-platform example application.
# Table of Contents
* [Chapter 1: Introduction to libigl]
* [Chapter 2: Discrete Geometric Quantities and
Operators](#chapter2:discretegeometricquantitiesandoperators)
* [201 Normals](#normals)
* [Per-face](#per-face)
* [Per-vertex](#per-vertex)
* [Per-corner](#per-corner)
* [202 Gaussian Curvature](#gaussiancurvature)
* [203 Curvature Directions](#curvaturedirections)
* [204 Gradient](#gradient)
* [204 Laplacian](#laplacian)
* [Mass matrix](#massmatrix)
* [Alternative construction of
Laplacian](#alternativeconstructionoflaplacian)
* [Chapter 3: Matrices and Linear Algebra](#chapter3:matricesandlinearalgebra)
* [301 Slice](#slice)
* [302 Sort](#sort)
* [Other Matlab-style functions](#othermatlab-stylefunctions)
* [303 Laplace Equation](#laplaceequation)
* [Quadratic energy minimization](#quadraticenergyminimization)
* [304 Linear Equality Constraints](#linearequalityconstraints)
* [305 Quadratic Programming](#quadraticprogramming)
* [Chapter 4: Shape Deformation](#chapter4:shapedeformation)
* [401 Biharmonic Deformation](#biharmonicdeformation)
* [402 Polyharmonic Deformation](#polyharmonicdeformation)
* [403 Bounded Biharmonic Weights](#boundedbiharmonicweights)
* [404 Dual Quaternion Skinning](#dualquaternionskinning)
* [405 As-rigid-as-possible](#as-rigid-as-possible)
* [406 Fast automatic skinning
transformations](#fastautomaticskinningtransformations)
# Chapter 2: Discrete Geometric Quantities and Operators
This chapter illustrates a few discrete quantities that libigl can compute on a
mesh. This also provides an introduction to basic drawing and coloring routines
in our example viewer. Finally, we construct popular discrete differential
geometry operators.
## Normals
Surface normals are a basic quantity necessary for rendering a surface. There
are a variety of ways to compute and store normals on a triangle mesh.
### Per-face
Normals are well defined on each triangle of a mesh as the vector orthogonal to
triangle's plane. These piecewise constant normals produce piecewise-flat
renderings: the surface appears non-smooth and reveals its underlying
discretization.
### Per-vertex
Storing normals at vertices, Phong or Gouraud shading will interpolate shading
inside mesh triangles to produce smooth(er) renderings. Most techniques for
computing per-vertex normals take an average of incident face normals. The
techniques vary with respect to their different weighting schemes. Uniform
weighting is heavily biased by the discretization choice, where as area-based
or angle-based weighting is more forgiving.
The typical half-edge style computation of area-based weights might look
something like this:
```cpp
N.setZero(V.rows(),3);
for(int i : vertices)
{
for(face : incident_faces(i))
{
N.row(i) += face.area * face.normal;
}
}
N.rowwise().normalize();
```
Without a half-edge data-structure it may seem at first glance that looping
over incident faces---and thus constructing the per-vertex normals---would be
inefficient. However, per-vertex normals may be _throwing_ each face normal to
running sums on its corner vertices:
```cpp
N.setZero(V.rows(),3);
for(int f = 0; f < F.rows();f++)
{
for(int c = 0; c < 3;c++)
{
N.row(F(f,c)) += area(f) * face_normal.row(f);
}
}
N.rowwise().normalize();
```
### Per-corner
Storing normals per-corner is an efficient an convenient way of supporting both
smooth and sharp (e.g. creases and corners) rendering. This format is common to
OpenGL and the .obj mesh file format. Often such normals are tuned by the mesh
designer, but creases and corners can also be computed automatically. Libigl
implements a simple scheme which computes corner normals as averages of
normals of faces incident on the corresponding vertex which do not deviate by a
specified dihedral angle (e.g. 20°).

## Gaussian Curvature
Gaussian curvature on a continuous surface is defined as the product of the
principal curvatures:
$k_G = k_1 k_2.$
As an _intrinsic_ measure, it depends on the metric and
not the surface's embedding.
Intuitively, Gaussian curvature tells how locally spherical or _elliptic_ the
surface is ( $k_G>0$ ), how locally saddle-shaped or _hyperbolic_ the surface
is ( $k_G<0$ ), or how locally cylindrical or _parabolic_ ( $k_G=0$ ) the
surface is.
In the discrete setting, one definition for a ``discrete Gaussian curvature''
on a triangle mesh is via a vertex's _angular deficit_:
$k_G(v_i) = 2π - \sum\limits_{j\in N(i)}θ_{ij},$
where $N(i)$ are the triangles incident on vertex $i$ and $θ_{ij}$ is the angle
at vertex $i$ in triangle $j$ [][#meyer_2003].
Just like the continuous analog, our discrete Gaussian curvature reveals
elliptic, hyperbolic and parabolic vertices on the domain.

## Curvature Directions
The two principal curvatures $(k_1,k_2)$ at a point on a surface measure how much the
surface bends in different directions. The directions of maximum and minimum
(signed) bending are call principal directions and are always
orthogonal.
Mean curvature is defined simply as the average of principal curvatures:
$H = \frac{1}{2}(k_1 + k_2).$
One way to extract mean curvature is by examining the Laplace-Beltrami operator
applied to the surface positions. The result is a so-called mean-curvature
normal:
$-\Delta \mathbf{x} = H \mathbf{n}.$
It is easy to compute this on a discrete triangle mesh in libigl using the cotangent
Laplace-Beltrami operator [][#meyer_2003].
```cpp
#include
#include
#include
...
MatrixXd HN;
SparseMatrix L,M,Minv;
igl::cotmatrix(V,F,L);
igl::massmatrix(V,F,igl::MASSMATRIX_TYPE_VORONOI,M);
igl::invert_diag(M,Minv);
HN = -Minv*(L*V);
H = (HN.rowwise().squaredNorm()).array().sqrt();
```
Combined with the angle defect definition of discrete Gaussian curvature, one
can define principal curvatures and use least squares fitting to find
directions [][#meyer_2003].
Alternatively, a robust method for determining principal curvatures is via
quadric fitting [][#pannozo_2010]. In the neighborhood
around every vertex, a best-fit quadric is found and principal curvature values
and directions are sampled from this quadric. With these in tow, one can
compute mean curvature and Gaussian curvature as sums and products
respectively.

This is an example of syntax highlighted code:
```cpp
#include
int main(int argc, char * argv[])
{
return 0;
}
```
## Gradient
Scalar functions on a surface can be discretized as a piecewise linear function
with values defined at each mesh vertex:
$f(\mathbf{x}) \approx \sum\limits_{i=0}^n \phi_i(\mathbf{x})\, f_i,$
where $\phi_i$ is a piecewise linear hat function defined by the mesh so that
for each triangle $\phi_i$ is _the_ linear function which is one only at
vertex $i$ and zero at the other corners.
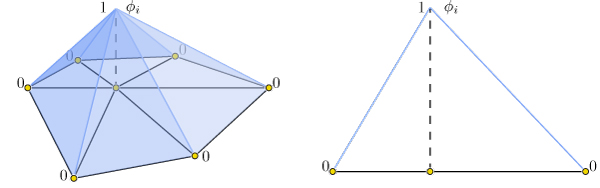
Thus gradients of such piecewise linear functions are simply sums of gradients
of the hat functions:
$\nabla f(\mathbf{x}) \approx
\nabla \sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i =
\sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i.$
This reveals that the gradient is a linear function of the vector of $f_i$
values. Because $\phi_i$ are linear in each triangle their gradient are
_constant_ in each triangle. Thus our discrete gradient operator can be written
as a matrix multiplication taking vertex values to triangle values:
$\nabla f \approx \mathbf{G}\,\mathbf{f},$
where $\mathbf{f}$ is $n\times 1$ and $\mathbf{G}$ is an $md\times n$ sparse
matrix. This matrix $\mathbf{G}$ can be derived geometrically, e.g.
[ch. 2][#jacobson_thesis_2013].
Libigl's `gradMat`**Alec: check name** function computes $\mathbf{G}$ for
triangle and tetrahedral meshes:

## Laplacian
The discrete Laplacian is an essential geometry processing tool. Many
interpretations and flavors of the Laplace and Laplace-Beltrami operator exist.
In open Euclidean space, the _Laplace_ operator is the usual divergence of gradient
(or equivalently the Laplacian of a function is the trace of its Hessian):
$\Delta f =
\frac{\partial^2 f}{\partial x^2} +
\frac{\partial^2 f}{\partial y^2} +
\frac{\partial^2 f}{\partial z^2}.$
The _Laplace-Beltrami_ operator generalizes this to surfaces.
When considering piecewise-linear functions on a triangle mesh, a discrete Laplacian may
be derived in a variety of ways. The most popular in geometry processing is the
so-called ``cotangent Laplacian'' $\mathbf{L}$, arising simultaneously from FEM, DEC and
applying divergence theorem to vertex one-rings. As a linear operator taking
vertex values to vertex values, the Laplacian $\mathbf{L}$ is a $n\times n$
matrix with elements:
$L_{ij} = \begin{cases}j \in N(i) &\cot \alpha_{ij} + \cot \beta_{ij},\\
j \notin N(i) & 0,\\
i = j & -\sum\limits_{k\neq i} L_{ik},
\end{cases}$
where $N(i)$ are the vertices adjacent to (neighboring) vertex $i$, and
$\alpha_{ij},\beta_{ij}$ are the angles opposite edge ${ij}$.
This oft
produced formula leads to a typical half-edge style implementation for
constructing $\mathbf{L}$:
```cpp
for(int i : vertices)
{
for(int j : one_ring(i))
{
for(int k : triangle_on_edge(i,j))
{
L(i,j) = cot(angle(i,j,k));
L(i,i) -= cot(angle(i,j,k));
}
}
}
```
Without a half-edge data-structure it may seem at first glance that looping
over one-rings, and thus constructing the Laplacian would be inefficient.
However, the Laplacian may be built by summing together contributions for each
triangle, much in spirit with its FEM discretization of the Dirichlet energy
(sum of squared gradients):
```cpp
for(triangle t : triangles)
{
for(edge i,j : t)
{
L(i,j) += cot(angle(i,j,k));
L(j,i) += cot(angle(i,j,k));
L(i,i) -= cot(angle(i,j,k));
L(j,j) -= cot(angle(i,j,k));
}
}
```
Libigl implements discrete "cotangent" Laplacians for triangles meshes and
tetrahedral meshes, building both with fast geometric rules rather than "by the
book" FEM construction which involves many (small) matrix inversions, cf.
**Alec: cite Ariel reconstruction paper**.
The operator applied to mesh vertex positions amounts to smoothing by _flowing_
the surface along the mean curvature normal direction. This is equivalent to
minimizing surface area.
![The `Laplacian` example computes conformalized mean curvature flow using the
cotangent Laplacian [#kazhdan_2012][].](images/cow-curvature-flow.jpg)
### Mass matrix
The mass matrix $\mathbf{M}$ is another $n \times n$ matrix which takes vertex
values to vertex values. From an FEM point of view, it is a discretization of
the inner-product: it accounts for the area around each vertex. Consequently,
$\mathbf{M}$ is often a diagonal matrix, such that $M_{ii}$ is the barycentric
or voronoi area around vertex $i$ in the mesh [#meyer_2003][]. The inverse of
this matrix is also very useful as it transforms integrated quantities into
point-wise quantities, e.g.:
$\nabla f \approx \mathbf{M}^{-1} \mathbf{L} \mathbf{f}.$
In general, when encountering squared quantities integrated over the surface,
the mass matrix will be used as the discretization of the inner product when
sampling function values at vertices:
$\int_S x\, y\ dA \approx \mathbf{x}^T\mathbf{M}\,\mathbf{y}.$
An alternative mass matrix $\mathbf{T}$ is a $md \times md$ matrix which takes
triangle vector values to triangle vector values. This matrix represents an
inner-product accounting for the area associated with each triangle (i.e. the
triangles true area).
### Alternative construction of Laplacian
An alternative construction of the discrete cotangent Laplacian is by
"squaring" the discrete gradient operator. This may be derived by applying
Green's identity (ignoring boundary conditions for the moment):
$\int_S \|\nabla f\|^2 dA = \int_S f \Delta f dA$
Or in matrix form which is immediately translatable to code:
$\mathbf{f}^T \mathbf{G}^T \mathbf{T} \mathbf{G} \mathbf{f} =
\mathbf{f}^T \mathbf{M} \mathbf{M}^{-1} \mathbf{L} \mathbf{f} =
\mathbf{f}^T \mathbf{L} \mathbf{f}.$
So we have that $\mathbf{L} = \mathbf{G}^T \mathbf{T} \mathbf{G}$. This also
hints that we may consider $\mathbf{G}^T$ as a discrete _divergence_ operator,
since the Laplacian is the divergence of gradient. Naturally, $\mathbf{G}^T$ is
$n \times md$ sparse matrix which takes vector values stored at triangle faces
to scalar divergence values at vertices.
# Chapter 3: Matrices and Linear Algebra
Libigl relies heavily on the Eigen library for dense and sparse linear algebra
routines. Besides geometry processing routines, libigl has a few linear algebra
routines which bootstrap Eigen and make Eigen feel even more like a high-level
algebra library like Matlab.
## Slice
A very familiar and powerful routine in Matlab is array slicing. This allows
reading from or writing to a possibly non-contiguous sub-matrix. Let's consider
the matlab code:
```matlab
B = A(R,C);
```
If `A` is a $m \times n$ matrix and `R` is a $j$-long list of row-indices
(between 1 and $m$) and `C` is a $k$-long list of column-indices, then as a
result `B` will be a $j \times k$ matrix drawing elements from `A` according to
`R` and `C`. In libigl, the same functionality is provided by the `slice`
function:
```cpp
VectorXi R,C;
MatrixXd A,B;
...
igl::slice(A,R,C,B);
```
`A` and `B` could also be sparse matrices.
Similarly, consider the matlab code:
```matlab
A(R,C) = B;
```
Now, the selection is on the left-hand side so the $j \times k$ matrix `B` is
being _written into_ the submatrix of `A` determined by `R` and `C`. This
functionality is provided in libigl using `slice_into`:
```cpp
igl::slice_into(B,R,C,A);
```

## Sort
Matlab and other higher-level languages make it very easy to extract indices of
sorting and comparison routines. For example in Matlab, one can write:
```matlab
[Y,I] = sort(X,1,'ascend');
```
so if `X` is a $m \times n$ matrix then `Y` will also be an $m \times n$ matrix
with entries sorted along dimension `1` in `'ascend'`ing order. The second
output `I` is a $m \times n$ matrix of indices such that `Y(i,j) =
X(I(i,j),j);`. That is, `I` reveals how `X` is sorted into `Y`.
This same functionality is supported in libigl:
```cpp
igl::sort(X,1,true,Y,I);
```
Similarly, sorting entire rows can be accomplished in matlab using:
```matlab
[Y,I] = sortrows(X,'ascend');
```
where now `I` is a $m$ vector of indices such that `Y = X(I,:)`.
In libigl, this is supported with
```cpp
igl::sortrows(X,true,Y,I);
```
where again `I` reveals the index of sort so that it can be reproduced with
`igl::slice(X,I,1,Y)`.
Analogous functions are available in libigl for: `max`, `min`, and `unique`.

### Other Matlab-style functions
Libigl implements a variety of other routines with the same api and
functionality as common matlab functions.
- `igl::any_of` Whether any elements are non-zero (true)
- `igl::cat` Concatenate two matrices (especially useful for dealing with Eigen
sparse matrices)
- `igl::ceil` Round entries up to nearest integer
- `igl::cumsum` Cumulative sum of matrix elements
- `igl::colon` Act like Matlab's `:`, similar to Eigen's `LinSpaced`
- `igl::cross` Cross product per-row
- `igl::dot` dot product per-row
- `igl::find` Find subscripts of non-zero entries
- `igl::floot` Round entries down to nearest integer
- `igl::histc` Counting occurrences for building a histogram
- `igl::hsv_to_rgb` Convert HSV colors to RGB (cf. Matlab's `hsv2rgb`)
- `igl::intersect` Set intersection of matrix elements.
- `igl::jet` Quantized colors along the rainbow.
- `igl::kronecker_product` Compare to Matlab's `kronprod`
- `igl::median` Compute the median per column
- `igl::mode` Compute the mode per column
- `igl::orth` Orthogonalization of a basis
- `igl::setdiff` Set difference of matrix elements
- `igl::speye` Identity as sparse matrix
## Laplace Equation
A common linear system in geometry processing is the Laplace equation:
$∆z = 0$
subject to some boundary conditions, for example Dirichlet boundary conditions
(fixed value):
$\left.z\right|_{\partial{S}} = z_{bc}$
In the discrete setting, this begins with the linear system:
$\mathbf{L} \mathbf{z} = \mathbf{0}$
where $\mathbf{L}$ is the $n \times n$ discrete Laplacian and $\mathbf{z}$ is a
vector of per-vertex values. Most of $\mathbf{z}$ correspond to interior
vertices and are unknown, but some of $\mathbf{z}$ represent values at boundary
vertices. Their values are known so we may move their corresponding terms to
the right-hand side.
Conceptually, this is very easy if we have sorted $\mathbf{z}$ so that interior
vertices come first and then boundary vertices:
$$\left(\begin{array}{cc}
\mathbf{L}_{in,in} & \mathbf{L}_{in,b}\\
\mathbf{L}_{b,in} & \mathbf{L}_{b,b}\end{array}\right)
\left(\begin{array}{c}
\mathbf{z}_{in}\\
\mathbf{L}_{b}\end{array}\right) =
\left(\begin{array}{c}
\mathbf{0}_{in}\\
\mathbf{*}_{b}\end{array}\right)$$
The bottom block of equations is no longer meaningful so we'll only consider
the top block:
$$\left(\begin{array}{cc}
\mathbf{L}_{in,in} & \mathbf{L}_{in,b}\end{array}\right)
\left(\begin{array}{c}
\mathbf{z}_{in}\\
\mathbf{z}_{b}\end{array}\right) =
\mathbf{0}_{in}$$
Where now we can move known values to the right-hand side:
$$\mathbf{L}_{in,in}
\mathbf{z}_{in} = -
\mathbf{L}_{in,b}
\mathbf{z}_{b}$$
Finally we can solve this equation for the unknown values at interior vertices
$\mathbf{z}_{in}$.
However, probably our vertices are not sorted. One option would be to sort `V`,
then proceed as above and then _unsort_ the solution `Z` to match `V`. However,
this solution is not very general.
With array slicing no explicit sort is needed. Instead we can _slice-out_
submatrix blocks ($\mathbf{L}_{in,in}$, $\mathbf{L}_{in,b}$, etc.) and follow
the linear algebra above directly. Then we can slice the solution _into_ the
rows of `Z` corresponding to the interior vertices.

### Quadratic energy minimization
The same Laplace equation may be equivalently derived by minimizing Dirichlet
energy subject to the same boundary conditions:
$\mathop{\text{minimize }}_z \frac{1}{2}\int\limits_S \|\nabla z\|^2 dA$
On our discrete mesh, recall that this becomes
$\mathop{\text{minimize }}_\mathbf{z} \frac{1}{2}\mathbf{z}^T \mathbf{G}^T \mathbf{D}
\mathbf{G} \mathbf{z} \rightarrow \mathop{\text{minimize }}_\mathbf{z} \mathbf{z}^T \mathbf{L} \mathbf{z}$
The general problem of minimizing some energy over a mesh subject to fixed
value boundary conditions is so wide spread that libigl has a dedicated api for
solving such systems.
Let's consider a general quadratic minimization problem subject to different
common constraints:
$$\mathop{\text{minimize }}_\mathbf{z} \frac{1}{2}\mathbf{z}^T \mathbf{Q} \mathbf{z} +
\mathbf{z}^T \mathbf{B} + \text{constant},$$
subject to
$$\mathbf{z}_b = \mathbf{z}_{bc} \text{ and } \mathbf{A}_{eq} \mathbf{z} =
\mathbf{B}_{eq},$$
where
- $\mathbf{Q}$ is a (usually sparse) $n \times n$ positive semi-definite
matrix of quadratic coefficients (Hessian),
- $\mathbf{B}$ is a $n \times 1$ vector of linear coefficients,
- $\mathbf{z}_b$ is a $|b| \times 1$ portion of
$\mathbf{z}$ corresponding to boundary or _fixed_ vertices,
- $\mathbf{z}_{bc}$ is a $|b| \times 1$ vector of known values corresponding to
$\mathbf{z}_b$,
- $\mathbf{A}_{eq}$ is a (usually sparse) $m \times n$ matrix of linear
equality constraint coefficients (one row per constraint), and
- $\mathbf{B}_{eq}$ is a $m \times 1$ vector of linear equality constraint
right-hand side values.
This specification is overly general as we could write $\mathbf{z}_b =
\mathbf{z}_{bc}$ as rows of $\mathbf{A}_{eq} \mathbf{z} =
\mathbf{B}_{eq}$, but these fixed value constraints appear so often that they
merit a dedicated place in the API.
In libigl, solving such quadratic optimization problems is split into two
routines: precomputation and solve. Precomputation only depends on the
quadratic coefficients, known value indices and linear constraint coefficients:
```cpp
igl::min_quad_with_fixed_data mqwf;
igl::min_quad_with_fixed_precompute(Q,b,Aeq,true,mqwf);
```
The output is a struct `mqwf` which contains the system matrix factorization
and is used during solving with arbitrary linear terms, known values, and
constraint right-hand sides:
```cpp
igl::min_quad_with_fixed_solve(mqwf,B,bc,Beq,Z);
```
The output `Z` is a $n \times 1$ vector of solutions with fixed values
correctly placed to match the mesh vertices `V`.
## Linear Equality Constraints
We saw above that `min_quad_with_fixed_*` in libigl provides a compact way to
solve general quadratic programs. Let's consider another example, this time
with active linear equality constraints. Specifically let's solve the
`bi-Laplace equation` or equivalently minimize the Laplace energy:
$$\Delta^2 z = 0 \leftrightarrow \mathop{\text{minimize }}\limits_z \frac{1}{2}
\int\limits_S (\Delta z)^2 dA$$
subject to fixed value constraints and a linear equality constraint:
$z_{a} = 1, z_{b} = -1$ and $z_{c} = z_{d}$.
Notice that we can rewrite the last constraint in the familiar form from above:
$z_{c} - z_{d} = 0.$
Now we can assembly `Aeq` as a $1 \times n$ sparse matrix with a coefficient
$1$
in the column corresponding to vertex $c$ and a $-1$ at $d$. The right-hand side
`Beq` is simply zero.
Internally, `min_quad_with_fixed_*` solves using the Lagrange Multiplier
method. This method adds additional variables for each linear constraint (in
general a $m \times 1$ vector of variables $\lambda$) and then solves the
saddle problem:
$$\mathop{\text{find saddle }}_{\mathbf{z},\lambda}\, \frac{1}{2}\mathbf{z}^T \mathbf{Q} \mathbf{z} +
\mathbf{z}^T \mathbf{B} + \text{constant} + \lambda^T\left(\mathbf{A}_{eq}
\mathbf{z} - \mathbf{B}_{eq}\right)$$
This can be rewritten in a more familiar form by stacking $\mathbf{z}$ and
$\lambda$ into one $(m+n) \times 1$ vector of unknowns:
$$\mathop{\text{find saddle }}_{\mathbf{z},\lambda}\,
\frac{1}{2}
\left(
\mathbf{z}^T
\lambda^T
\right)
\left(
\begin{array}{cc}
\mathbf{Q} & \mathbf{A}_{eq}^T\\
\mathbf{A}_{eq} & 0
\end{array}
\right)
\left(
\begin{array}{c}
\mathbf{z}\\
\lambda
\end{array}
\right) +
\left(
\mathbf{z}^T
\lambda^T
\right)
\left(
\begin{array}{c}
\mathbf{B}\\
-\mathbf{B}_{eq}
\end{array}
\right)
+ \text{constant}$$
Differentiating with respect to $\left( \mathbf{z}^T \lambda^T \right)$ reveals
a linear system and we can solve for $\mathbf{z}$ and $\lambda$. The only
difference from
the straight quadratic
_minimization_ system, is that
this saddle problem system will not be positive definite. Thus, we must use a
different factorization technique (LDLT rather than LLT). Luckily, libigl's
`min_quad_with_fixed_precompute` automatically chooses the correct solver in
the presence of linear equality constraints.

## Quadratic Programming
We can generalize the quadratic optimization in the previous section even more
by allowing inequality constraints. Specifically box constraints (lower and
upper bounds):
$\mathbf{l} \le \mathbf{z} \le \mathbf{u},$
where $\mathbf{l},\mathbf{u}$ are $n \times 1$ vectors of lower and upper
bounds
and general linear inequality constraints:
$\mathbf{A}_{ieq} \mathbf{z} \le \mathbf{B}_{ieq},$
where $\mathbf{A}_{ieq}$ is a $k \times n$ matrix of linear coefficients and
$\mathbf{B}_{ieq}$ is a $k \times 1$ matrix of constraint right-hand sides.
Again, we are overly general as the box constraints could be written as
rows of the linear inequality constraints, but bounds appear frequently enough
to merit a dedicated api.
Libigl implements its own active set routine for solving _quadratric programs_
(QPs). This algorithm works by iteratively "activating" violated inequality
constraints by enforcing them as equalities and "deactivating" constraints
which are no longer needed.
After deciding which constraints are active each iteration simple reduces to a
quadratic minimization subject to linear _equality_ constraints, and the method
from the previous section is invoked. This is repeated until convergence.
Currently the implementation is efficient for box constraints and sparse
non-overlapping linear inequality constraints.
Unlike alternative interior-point methods, the active set method benefits from
a warm-start (initial guess for the solution vector $\mathbf{z}$).
```cpp
igl::active_set_params as;
// Z is optional initial guess and output
igl::active_set(Q,B,b,bc,Aeq,Beq,Aieq,Bieq,lx,ux,as,Z);
```
![The example `QuadraticProgramming` uses an active set solver to optimize
discrete biharmonic kernels at multiple scales [#rustamov_2011][].](images/cheburashka-multiscale-biharmonic-kernels.jpg)
# Chapter 4: Shape Deformation
Modern mesh-based shape deformation methods satisfy user deformation
constraints at handles (selected vertices or regions on the mesh) and propagate
these handle deformations to the rest of shape _smoothly_ and _without removing
or distorting details_. Libigl provides implementations of a variety of
state-of-the-art deformation techniques, ranging from quadratic mesh-based
energy minimizers, to skinning methods, to non-linear elasticity-inspired
techniques.
## Biharmonic Deformation
The period of research between 2000 and 2010 produced a collection of
techniques that cast the problem of handle-based shape deformation as a
quadratic energy minimization problem or equivalently the solution to a linear
partial differential equation.
There are many flavors of these techniques, but
a prototypical subset are those that consider solutions to the bi-Laplace
equation, that is biharmonic functions [#botsch_2004][]. This fourth-order PDE provides
sufficient flexibility in boundary conditions to ensure $C^1$ continuity at
handle constraints (in the limit under refinement) [#jacobson_mixed_2010][].
### Biharmonic surfaces
Let us first begin our discussion of biharmonic _deformation_, by considering
biharmonic _surfaces_. We will casually define biharmonic surfaces as surface
whose _position functions_ are biharmonic with respect to some initial
parameterization:
$\Delta \mathbf{x}' = 0$
and subject to some handle constraints, conceptualized as "boundary
conditions":
$\mathbf{x}'_{b} = \mathbf{x}_{bc}.$
where $\mathbf{x}'$ is the unknown 3D position of a point on the surface. So we are
asking that the bi-Laplace of each of spatial coordinate functions to be zero.
In libigl, one can solve a biharmonic problem like this with `igl::harmonic`
and setting $k=2$ (_bi_-harmonic):
```cpp
// U_bc contains deformation of boundary vertices b
igl::harmonic(V,F,b,U_bc,2,U);
```
This produces smooth surfaces that interpolate the handle constraints, but all
original details on the surface will be _smoothed away_. Most obviously, if the
original surface is not already biharmonic, then giving all handles the identity
deformation (keeping them at their rest positions) will **not** reproduce the
original surface. Rather, the result will be the biharmonic surface that does
interpolate those handle positions.
Thus, we may conclude that this is not an intuitive technique for shape
deformation.
### Biharmonic deformation fields
Now we know that one useful property for a deformation technique is "rest pose
reproduction": applying no deformation to the handles should apply no
deformation to the shape.
To guarantee this by construction we can work with _deformation fields_ (ie.
displacements)
$\mathbf{d}$ rather
than directly with positions $\mathbf{x}. Then the deformed positions can be
recovered as
$\mathbf{x}' = \mathbf{x}+\mathbf{d}.$
A smooth deformation field $\mathbf{d}$ which interpolates the deformation
fields of the handle constraints will impose a smooth deformed shape
$\mathbf{x}'$. Naturally, we consider _biharmonic deformation fields_:
$\Delta \mathbf{d} = 0$
subject to the same handle constraints, but rewritten in terms of their implied
deformation field at the boundary (handles):
$\mathbf{d}_b = \mathbf{x}_{bc} - \mathbf{x}_b.$
Again we can use `igl::harmonic` with $k=2$, but this time solve for the
deformation field and then recover the deformed positions:
```cpp
// U_bc contains deformation of boundary vertices b
D_bc = U_bc - igl::slice(V,b,1);
igl::harmonic(V,F,b,D_bc,2,D);
U = V+D;
```

#### Relationship to "differential coordinates" and Laplacian surface editing
Biharmonic functions (whether positions or displacements) are solutions to the
bi-Laplace equation, but also minimizers of the "Laplacian energy". For
example, for displacements $\mathbf{d}$, the energy reads
$\int\limits_S \|\Delta \mathbf{d}\|^2 dA.$
By linearity of the Laplace(-Beltrami) operator we can reexpress this energy in
terms of the original positions $\mathbf{x}$ and the unknown positions
$\mathbf{x}' = \mathbf{x} - \mathbf{d}$:
$\int\limits_S \|\Delta (\mathbf{x}' - \mathbf{x})\|^2 dA = \int\limits_S \|\Delta \mathbf{x}' - \Delta \mathbf{x})\|^2 dA.$
In the early work of Sorkine et al., the quantities $\Delta \mathbf{x}'$ and
$\Delta \mathbf{x}$ were dubbed "differential coordinates" [#sorkine_2004][].
Their deformations (without linearized rotations) is thus equivalent to
biharmonic deformation fields.
## Polyharmonic deformation
We can generalize biharmonic deformation by considering different powers of
the Laplacian, resulting in a series of PDEs of the form:
$\Delta^k \mathbf{d} = 0.$
with $k\in{1,2,3,\dots}$. The choice of $k$ determines the level of continuity
at the handles. In particular, $k=1$ implies $C^0$ at the boundary, $k=2$
implies $C^1$, $k=3$ implies $C^2$ and in general $k$ implies $C^{k-1}$.
```cpp
int k = 2;// or 1,3,4,...
igl::harmonic(V,F,b,bc,k,Z);
```

## Bounded Biharmonic Weights
In computer animation, shape deformation is often referred to as "skinning".
Constraints are posed as relative rotations of internal rigid "bones" inside a
character. The deformation method, or skinning method, determines how the
surface of the character (i.e. its skin) should move as a function of the bone
rotations.
The most popular technique is linear blend skinning. Each point on the shape
computes its new location as a linear combination of bone transformations:
$\mathbf{x}' = \sum\limits_{i = 0}^m w_i(\mathbf{x}) \mathbf{T}_i
\left(\begin{array}{c}\mathbf{x}_i\\1\end{array}\right),$
where $w_i(\mathbf{x})$ is the scalar _weight function_ of the ith bone evaluated at
$\mathbf{x}$ and $\mathbf{T}_i$ is the bone transformation as a $4 \times 3$
matrix.
This formula is embarassingly parallel (computation at one point does not
depend on shared data need by computation at another point). It is often
implemented as a vertex shader. The weights and rest positions for each vertex
are sent as vertex shader _attribtues_ and bone transformations are sent as
_uniforms_. Then vertices are transformed within the vertex shader, just in
time for rendering.
As the skinning formula is linear (hence its name), we can write it as matrix
multiplication:
$\mathbf{X}' = \mathbf{M} \mathbf{T},$
where $\mathbx{X}'$ is $n \times 3$ stack of deformed positions as row
vectors, $\mathbf{M}$ is a $n \times m\cdot dim$ matrix containing weights and
rest positions and $\mathbf{T}$ is a $m\cdot (dim+1) \times dim$ stack of
transposed bone transformations.
Traditionally, the weight functions $w_j$ are painted manually by skilled
rigging professionals. Modern techniques now exist to compute weight functions
automatically given the shape and a description of the skeleton (or in general
any handle structure such as a cage, collection of points, selected regions,
etc.).
Bounded biharmonic weights are one such technique that casts weight computation
as a constrained optimization problem [#jacobson_2011][]. The weights enforce
smoothness by minimizing a smoothness energy: the familiar Laplacian energy:
$\sum\limits_{i = 0}^m \int_S (\Delta w_i)^2 dA$
subject to constraints which enforce interpolation of handle constraints:
$w_i(\mathbf{x}) = \begin{cases} 1 & \text{ if } \mathbf{x} \in H_i\\ 0 & \text{ otherwise }
\end{cases},$
where $H_i$ is the ith handle, and constraints which enforce non-negativity,
parition of unity and encourage sparsity:
$0\le w_i \le 1$ and $\sum\limits_{i=0}^m w_i = 1.$
This is a quadratic programming problem and libigl solves it using its active
set solver or by calling out to Mosek.

[#botsch_2004]: Matrio Botsch and Leif Kobbelt. "An Intuitive Framework for
Real-Time Freeform Modeling," 2004.
[#jacobson_thesis_2013]: Alec Jacobson,
_Algorithms and Interfaces for Real-Time Deformation of 2D and 3D Shapes_,
2013.
[#jacobson_2011]: Alec Jacobson, Ilya Baran, Jovan Popović, and Olga Sorkin.
"Bounded Biharmonic Weights for Real-Time Deformation," 2011.
[#jacobson_mixed_2010]: Alec Jacobson, Elif Tosun, Olga Sorkine, and Denis
Zorin. "Mixed Finite Elements for Variational Surface Modeling," 2010.
[#kazhdan_2012]: Michael Kazhdan, Jake Solomon, Mirela Ben-Chen,
"Can Mean-Curvature Flow Be Made Non-Singular," 2012.
[#meyer_2003]: Mark Meyer, Mathieu Desbrun, Peter Schröder and Alan H. Barr,
"Discrete Differential-Geometry Operators for Triangulated
2-Manifolds," 2003.
[#pannozo_2010]: Daniele Pannozo, Enrico Puppo, Luigi Rocca,
"Efficient Multi-scale Curvature and Crease Estimation," 2010.
[#rustamov_2011]: Raid M. Rustamov, "Multiscale Biharmonic Kernels", 2011.
[#sorkine_2004]: Olga Sorkine, Yaron Lipman, Daniel Cohen-Or, Marc Alexa,
Christian Rössl and Hans-Peter Seidel. "Laplacian Surface Editing," 2004.