add beginning to the SIR section

chapters/chap02/chap02.tex

@@ -5,101 +5,217 @@
 % Part:     theoretical background
 % Description:
 %         summary of the content in this chapter
-% Version:  30.07.2024
+% Version:  02.08.2024
 % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 \chapter{Theoretical Background}
 \label{chap:background}
 
 This chapter introduces the theoretical knowledge that forms the foundation of
-the work presented in this thesis. In sections~\ref{sec:domain}
+the work presented in this thesis. In Sections~\ref{sec:domain}
 and~\ref{sec:differentialEq}, we talk about differential equations and the
-underlying theory. In these sections both the explanations and the approach are
+underlying theory. In these Sections both the explanations and the approach are
 strongly based on the book on analysis by Rudin~\cite{Rudin2007} and the book
 about ordinary differential equations by Tenenbaum and
 Pollard~\cite{Tenenbaum1985}. Subsequently, we employ this knowledge to examine
-various pandemic models in section~\ref{sec:epidemModel}.
+various pandemic models in Section~\ref{sec:epidemModel}.
 Finally, we address the topic of neural networks with a focus on the multilayer
-perceptron in section~\ref{sec:mlp} and physics informed neural networks in
-section~\ref{sec:pinn}.
+perceptron in Section~\ref{sec:mlp} and physics informed neural networks in
+Section~\ref{sec:pinn}.
 
 % -------------------------------------------------------------------
 
 \section{Mathematical Modelling using Functions}
 \label{sec:domain}
 
-In order to model a mathematical problem, it is necessary to define a set of fundamental numbers or quantities upon which the subsequent calculations will be based. These sets may
-represent, for instance, a specific time interval or a distance. The term \emph{domain} describes these fundamental sets of numbers or quantities~\cite{Rudin2007}. A \emph{variable}
-is a changing entity living in a certain domain. In this thesis,
-we will focus on domains of real numbers in $\mathbb{R}$.\\
-
-The mapping between variables enables the modeling of the process and depicts the semantics. We use functions in order to facilitate this mapping. Let $A, B\subset\mathbb{R}$ be to subsets
-of the real numbers, then we define a function as the mapping
+In order to model a mathematical problem, it is necessary to define a set of
+fundamental numbers or quantities upon which the subsequent calculations will be
+based. These sets may represent, for instance, a specific time interval or a
+distance. The term \emph{domain} describes these fundamental sets of numbers or
+quantities~\cite{Rudin2007}. A \emph{variable} is a changing entity living in a
+certain domain. In this thesis, we will focus on domains of real numbers in
+$\mathbb{R}$.\\
+
+The mapping between variables enables the modeling of the process and depicts
+the semantics. We use functions in order to facilitate this mapping. Let
+$A, B\subset\mathbb{R}$ be to subsets of the real numbers, then we define a
+function as the mapping
 \begin{equation}
   f: A\rightarrow B.
 \end{equation}
-In other words, the function $f$ maps elements $x\in A$ to values $f(x)\in B$. $A$ is the \emph{domain} of $f$, while $B$ is the \emph{codomain} of $f$. Functions are capable of representing
-the state of a system as a value based on an input value from their domain. One illustrative example is a function that maps a time point to the distance covered since a starting point. In this
-case, time serves as the domain, while the distance is the codomain.
+In other words, the function $f$ maps elements $x\in A$ to values
+$f(x)\in B$. $A$ is the \emph{domain} of $f$, while $B$ is the \emph{codomain}
+of $f$. Functions are capable of representing the state of a system as a value
+based on an input value from their domain. One illustrative example is a
+function that maps a time point to the distance covered since a starting point.
+In this case, time serves as the domain, while the distance is the codomain.
 
 % -------------------------------------------------------------------
 
 \section{Basics of Differential Equations}
 \label{sec:differentialEq}
 
-Often, the change of a system is more interesting than its current state. Functions are able to give us the latter, but only passively give information about the change of a system.
-The objective is to determine an effective method for calculating the change of a function across its domain. Let $f$ be a function and $[a, b]\subset \mathbb{R}$ an interval of real numbers,
-the expression
+Often, the change of a system is more interesting than its current state.
+Functions are able to give us the latter, but only passively give information
+about the change of a system. The objective is to determine an effective method
+for calculating the change of a function across its domain. Let $f$ be a
+function and $[a, b]\subset \mathbb{R}$ an interval of real numbers, the
+expression
 \begin{equation}
   m = \frac{f(b) - f(a)}{a-b}
 \end{equation}
-gives the average rate of change. While the average rate of change is useful in many cases, the momentary rate of change is more accurate. To calculate this, we need to
-narrow down, the interval to an infinitesimal. For each $x\in[a, b]$ we calculate
+gives the average rate of change. While the average rate of change is useful in
+many cases, the momentary rate of change is more accurate. To calculate this,
+we need to narrow down, the interval to an infinitesimal. For each $x\in[a, b]$
+we calculate
 \begin{equation} \label{eqn:differential}
   \frac{df}{dx} = \lim_{t\to x} \frac{f(t) - f(x)}{t-x},
 \end{equation}
-if it exists. $\frac{df}{dx}$ is the \emph{derivative}, or \emph{differential equation}, it returns the momentary rate of change of $f$ for each value $x$ of $f$'s
-domain. Repeating this process on $\frac{df}{dx}$ yields $\frac{d^2f}{dx^2}$, which is the function that calculates the rate of change of the rate of change and is called the second order
-derivative. Iterating this $n$ times results in $\frac{d^nf}{dx^n}$, the derivative of the $n$'th order. Another method for obtaining a differential equation is to create it from the semantics
-of a problem. This method is useful if no basic function exists for a system.\\
-
-In the context of functions, it is possible to have multiple domains, meaning that function has more than one parameter. To illustrate, consider a function operating in two-dimensional space,
-wherein each parameter represents one axis or one that, employs with time and locations as inputs. The term \emph{partial differential equations} (\emph{PDE}'s) describes differential equations
-of such functions, which require a derivative for each of their domains. In contrast, \emph{ordinary differential equations} (\emph{ODE}'s) are the single derivatives for a function having only
-one domain. In this thesis, we only need ODE's.\\
-
-A \emph{differential system} is the name for a collective of differential equations. The derivatives in a differential system each have their own codomain, which is part of the problem, while they
-all share the same domain.\\
-
-Tenenbaum and Pollard~\cite{Tenenbaum1985} provides many examples for ODE's, including the \emph{Motion of a Particle Along a Straight Line}. Newton's second law states that ``the rate of change of
-the momentum of a body ($momentum = mass \cdot velocity$) is proportional to the resultant external force $F$ acted upon it''~\cite{Tenenbaum1985}. Let $m$ be the mass of the body in kilograms, $v$ its velocity in seconds
-per meter and $t$ the time in seconds. Then, Newton's second law translates mathematically to
+if it exists. $\frac{df}{dx}$ is the \emph{derivative}, or
+\emph{differential equation}, it returns the momentary rate of change of $f$ for
+each value $x$ of $f$'s domain. Repeating this process on $\frac{df}{dx}$ yields
+$\frac{d^2f}{dx^2}$, which is the function that calculates the rate of change of
+the rate of change and is called the second order derivative. Iterating this $n$
+times results in $\frac{d^nf}{dx^n}$, the derivative of the $n$'th order.
+Another method for obtaining a differential equation is to create it from the
+semantics of a problem. This method is useful if no basic function exists for a
+system.\\
+
+In the context of functions, it is possible to have multiple domains, meaning
+that function has more than one parameter. To illustrate, consider a function
+operating in two-dimensional space, wherein each parameter represents one axis
+or one that, employs with time and locations as inputs. The term
+\emph{partial differential equations} (\emph{PDE}'s) describes differential
+equations of such functions, which require a derivative for each of their
+domains. In contrast, \emph{ordinary differential equations} (\emph{ODE}'s) are
+the single derivatives for a function having only one domain. In this thesis, we
+only need ODE's.\\
+
+A \emph{differential system} is the name for a collective of differential
+equations. The derivatives in a differential system each have their own
+codomain, which is part of the problem, while they all share the same domain.\\
+
+Tenenbaum and Pollard~\cite{Tenenbaum1985} provides many examples for ODE's,
+including the \emph{Motion of a Particle Along a Straight Line}. Newton's second
+law states that ``the rate of change of the momentum of a body
+($momentum = mass \cdot velocity$) is proportional to the resultant external
+force $F$ acted upon it''~\cite{Tenenbaum1985}. Let $m$ be the mass of the body
+in kilograms, $v$ its velocity in seconds per meter and $t$ the time in seconds.
+Then, Newton's second law translates mathematically to
 \begin{equation} \label{eq:newtonSecLaw}
   F = m\frac{dv}{dt}.
 \end{equation}
-It is evident that the acceleration, $a=\frac{dv}{dt}$, as the rate of change of the velocity is part of the equation. Additionally, is the velocity of a body the derivative of the distance traveled
-by that body. Based on these findings, we can rewrite the equation~\ref{eq:newtonSecLaw} to
+It is evident that the acceleration, $a=\frac{dv}{dt}$, as the rate of change of
+the velocity is part of the equation. Additionally, is the velocity of a body
+the derivative of the distance traveled by that body. Based on these findings,
+we can rewrite the equation~\ref{eq:newtonSecLaw} to
 \begin{equation}
   F=ma=m\frac{d^2s}{dt^2}.
 \end{equation}
 
-
 % -------------------------------------------------------------------
 
 \section{Epidemiological Models}
 \label{sec:epidemModel}
 
-After a pandemic like \emph{COVID-19}, which has resulted in a significant number of fatalities, the question remains: How should we fight a pandemic correctly. Also, it is necessary to study whether the employed countermeasures efficacious in
-combating the pandemic. In the light of the unfavorable public responce to measures such as lockdowns, it is imperative to investigate that their efficacy remains commensurate with the costs incurred to those affected. In the event that
-alternative and novel technologies were in use, such as the mRNA vaccines in the context of COVID-19, it is needful to test the effect and find the optimal variant. In order to conduct the aforementioned investigations we to develop a
-method to quantize the pandemic and its course of progression. The real world is a highly complex system, which presents a significant challenge attempting to describe it fully in a model. The model must therefor reduce the complexity while retaining
-the essential information. Furthermore, it must address the issue of limited data availability. For instance, during COVID-19 institutions such as the Robert Koch Institute (RKI) were only able to collect data on infections and mortality cases.
-Consequently, we require a model that employs an abstraction of the real world to illustrate the events and relations that are pivotal to understanding the problem.
+After a pandemic like \emph{COVID-19}, which has resulted in a significant
+number of fatalities, the question remains: How should we fight a pandemic
+correctly. Also, it is necessary to study whether the employed countermeasures
+efficacious in combating the pandemic. In the light of the unfavorable public
+responce to measures such as lockdowns, it is imperative to investigate that
+their efficacy remains commensurate with the costs incurred to those affected.
+In the event that alternative and novel technologies were in use, such as the
+mRNA vaccines in the context of COVID-19, it is needful to test the effect and
+find the optimal variant. In order to conduct the aforementioned investigations
+we need to develop a method to quantize the pandemic and its course of progression.
+The real world is a highly complex system, which presents a significant
+challenge attempting to describe it fully in a model. The model must therefor
+reduce the complexity while retaining the essential information. Furthermore, it
+must address the issue of limited data availability. For instance, during
+COVID-19 institutions such as the Robert Koch Institute (RKI) were only able to
+collect data on infections and mortality cases. Consequently, we require a model
+that employs an abstraction of the real world to illustrate the events and
+relations that are pivotal to understanding the problem.
 
 % -------------------------------------------------------------------
 
 \subsection{SIR Model}
 \label{sec:pandemicModel:sir}
 
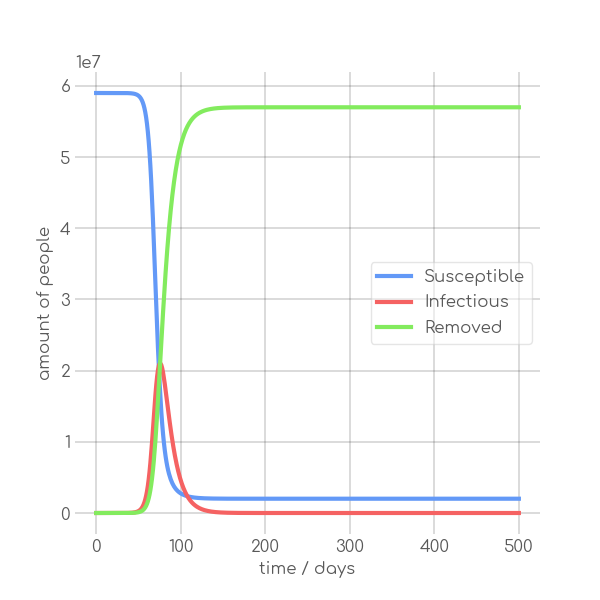
+One of the most influential epidemiological models is the \emph{SIR Model}
+introduced by Kermack and McKendrick~\cite{1927} in 1927. The book
+\emph{Mathematical Models in Biology}~\cite{EdelsteinKeshet2005} re-iterates the
+model and the following explanation will be based on it.\\
+
+The SIR Model is able to depict diseases, which are transferred by contact or
+close proximity of an individual carrying the illness and a healthy one. This is
+possible due to the distinction between infected beings carrying the disease and
+the group if people that are healthy but can be infected. In the model the
+mentioned are able to change, by healthy individuals getting infected. In the
+real world the size of a population has many causes to change. Births increase
+the population, while deaths make it decease. There are different reasons for
+people dying, for instance old age, or another disease. To omit this factor of
+complexity, the model assumes the size $N$ of the population is constant across
+the duration of the epidemic. Three groups make up the population $N$: the
+\emph{susceptible} group $S$, the \emph{infectious} group $I$ and the
+\emph{removed} group $R$ (hence SIR Model). For $S$, $I$, $R$ and $N$ applies:
+\begin{equation}
+  N = S + I + R.
+\end{equation}
+The model makes another assumption by stating that
+recovered people are immune to the illness and infectious individual can not
+infect them. The individuals in the $R$ group are either recovered and dead,
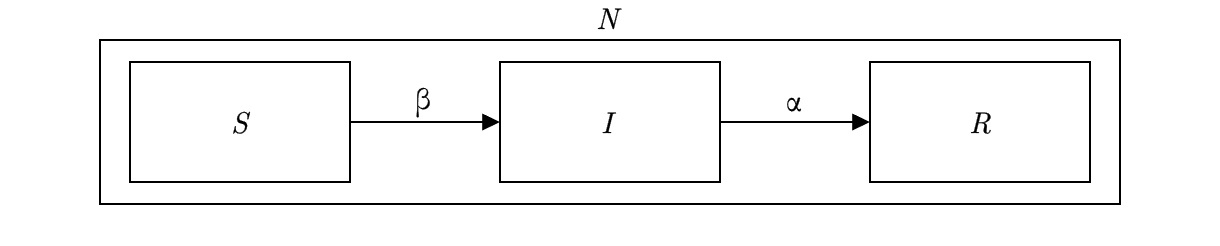
+which both cannot carry the disease anymore. As visualized in the
+Figure~\ref{fig:sir_model} the individuals can traverse from one group to
+another on the bases of rates. The transmission rate $\beta$ is responsible for
+people being infected, while the rate of removal or recovery rate $\alpha$
+(in literature also $\delta$ or $\nu$) moves people from $I$ to $R$.
+\begin{figure}[h]
+  \centering
+  \includegraphics[scale=0.3]{sir_graph.png}
+  \caption{SIR Model}
+  \label{fig:sir_model}
+\end{figure}
+
+\begin{figure}
+  \centering
+  \begin{subfigure}[b]{0.3\textwidth}
+    \centering
+    \includegraphics[width=\textwidth]{synth_alpha_beta}
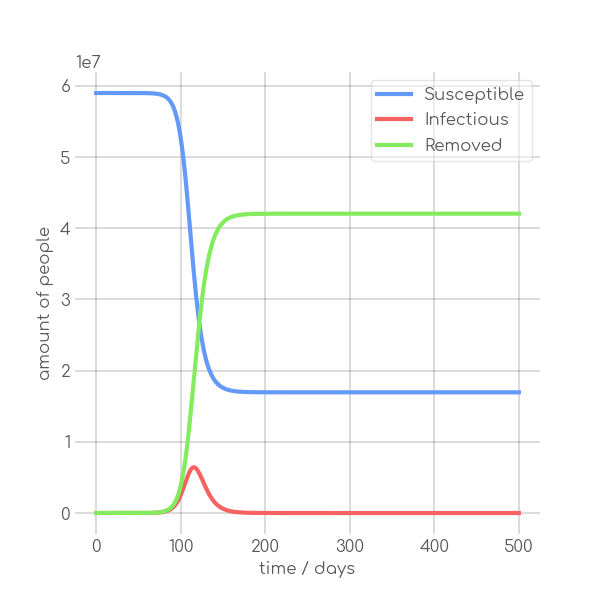
+    \caption{Basic configuration, $\alpha=0.35$, $\beta=0.2$}
+    \label{fig:synth_norm}
+  \end{subfigure}
+  \hfill
+  \begin{subfigure}[b]{0.3\textwidth}
+    \centering
+    \includegraphics[width=\textwidth]{synth_alpha_high_beta}
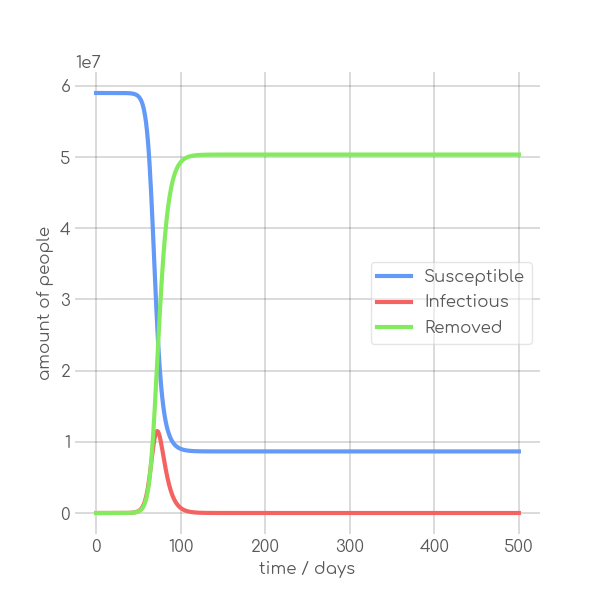
+    \caption{High $\alpha$ configuration, $\alpha=0.45$, $\beta=0.2$}
+    \label{fig:synth_high_beta}
+  \end{subfigure}
+  \hfill
+  \begin{subfigure}[b]{0.3\textwidth}
+    \centering
+    \includegraphics[width=\textwidth]{synth_alpha_low_beta}
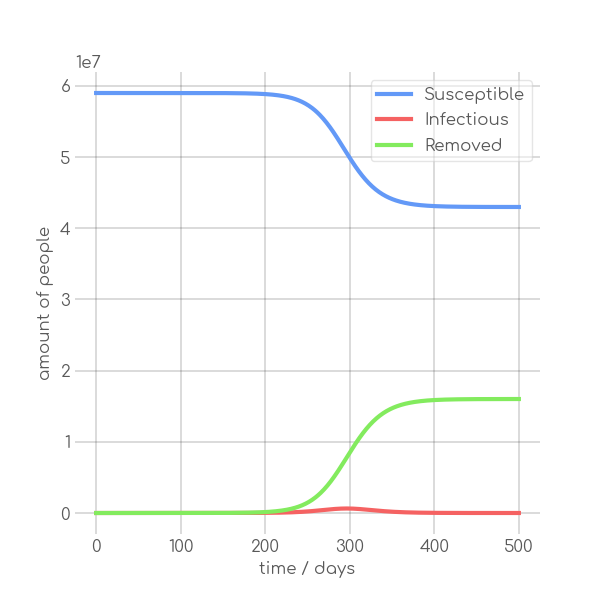
+    \caption{Low $\alpha$ configuration, $\alpha=0.25$, $\beta=0.2$}
+    \label{fig:synth_low_beta}
+  \end{subfigure}
+  \hfill
+  \begin{subfigure}[h]{0.3\textwidth}
+    \centering
+    \includegraphics[width=\textwidth]{synth_high_alpha_beta}
+    \caption{High $\beta$ configuration, $\alpha=0.35$, $\beta=0.3$}
+    \label{fig:synth_high_alpha}
+  \end{subfigure}
+  \hfill
+  \begin{subfigure}[h]{0.3\textwidth}
+    \centering
+    \includegraphics[width=\textwidth]{synth_low_alpha_beta}
+    \caption{Low $\beta$ configuration, $\alpha=0.35$, $\beta=0.1$}
+    \label{fig:synth_low_alpha}
+  \end{subfigure}
+  \caption{Synthetic data with different sets of parameters.}
+  \label{fig:synth_sir}
+\end{figure}
+
 % -------------------------------------------------------------------
 
 \subsection{reduced SIR Model}

thesis.bbl

@@ -7,6 +7,21 @@
   \providecommand{\doi}[1]{doi: #1}\else
   \providecommand{\doi}{doi: \begingroup \urlstyle{rm}\Url}\fi
 
+\bibitem[EK05]{EdelsteinKeshet2005}
+\textsc{Edelstein-Keshet}, Leah:
+\newblock \emph{Mathematical Models in Biology}.
+\newblock Society for Industrial and Applied Mathematics, 2005
+
+\bibitem[KM27]{1927}
+\textsc{Kermack}, William~O. ; \textsc{McKendrick}, A.~G.:
+\newblock A contribution to the mathematical theory of epidemics.
+\newblock {In: }\emph{Proceedings of the Royal Society of London. Series A,
+  Containing Papers of a Mathematical and Physical Character} 115 (1927),
+  August, Nr. 772, S. 700--721.
+\newblock \url{http://dx.doi.org/10.1098/rspa.1927.0118}. --
+\newblock DOI 10.1098/rspa.1927.0118. --
+\newblock ISSN 2053--9150
+
 \bibitem[Rud07]{Rudin2007}
 \textsc{Rudin}, Walter:
 \newblock \emph{Analysis}.

thesis.bib

@@ -77,4 +77,11 @@
   year      = {1985}
 }
 
+@Book{EdelsteinKeshet2005,
+  author    = {Leah Edelstein-Keshet},
+  publisher = {Society for Industrial and Applied Mathematics},
+  title     = {Mathematical Models in Biology},
+  year      = {2005},
+}
+
 @Comment{jabref-meta: databaseType:bibtex;}