|
@@ -11,16 +11,16 @@
|
|
|
\label{chap:background}
|
|
\label{chap:background}
|
|
|
|
|
|
|
|
This chapter introduces the theoretical knowledge that forms the foundation of
|
|
This chapter introduces the theoretical knowledge that forms the foundation of
|
|
|
-the work presented in this thesis. In Sections~\ref{sec:domain}
|
|
|
|
|
-and~\ref{sec:differentialEq}, we talk about differential equations and the
|
|
|
|
|
|
|
+the work presented in this thesis. In~\Cref{sec:domain}
|
|
|
|
|
+and~\Cref{sec:differentialEq}, we talk about differential equations and the
|
|
|
underlying theory. In these Sections both the explanations and the approach are
|
|
underlying theory. In these Sections both the explanations and the approach are
|
|
|
strongly based on the book on analysis by Rudin~\cite{Rudin2007} and the book
|
|
strongly based on the book on analysis by Rudin~\cite{Rudin2007} and the book
|
|
|
about ordinary differential equations by Tenenbaum and
|
|
about ordinary differential equations by Tenenbaum and
|
|
|
Pollard~\cite{Tenenbaum1985}. Subsequently, we employ this knowledge to examine
|
|
Pollard~\cite{Tenenbaum1985}. Subsequently, we employ this knowledge to examine
|
|
|
-various pandemic models in Section~\ref{sec:epidemModel}.
|
|
|
|
|
|
|
+various pandemic models in~\Cref{sec:epidemModel}.
|
|
|
Finally, we address the topic of neural networks with a focus on the multilayer
|
|
Finally, we address the topic of neural networks with a focus on the multilayer
|
|
|
-perceptron in Section~\ref{sec:mlp} and physics informed neural networks in
|
|
|
|
|
-Section~\ref{sec:pinn}.
|
|
|
|
|
|
|
+perceptron in~\Cref{sec:mlp} and physics informed neural networks
|
|
|
|
|
+in~\Cref{sec:pinn}.
|
|
|
|
|
|
|
|
% -------------------------------------------------------------------
|
|
% -------------------------------------------------------------------
|
|
|
|
|
|
|
@@ -109,7 +109,7 @@ Then, Newton's second law translates mathematically to
|
|
|
It is evident that the acceleration, $a=\frac{dv}{dt}$, as the rate of change of
|
|
It is evident that the acceleration, $a=\frac{dv}{dt}$, as the rate of change of
|
|
|
the velocity is part of the equation. Additionally, the velocity of a body is
|
|
the velocity is part of the equation. Additionally, the velocity of a body is
|
|
|
the derivative of the distance traveled by that body. Based on these findings,
|
|
the derivative of the distance traveled by that body. Based on these findings,
|
|
|
-we can rewrite the equation~\ref{eq:newtonSecLaw} to
|
|
|
|
|
|
|
+we can rewrite the~\Cref{eq:newtonSecLaw} to
|
|
|
\begin{equation}
|
|
\begin{equation}
|
|
|
F=ma=m\frac{d^2s}{dt^2}.
|
|
F=ma=m\frac{d^2s}{dt^2}.
|
|
|
\end{equation}\\
|
|
\end{equation}\\
|
|
@@ -153,26 +153,27 @@ and relations that are pivotal to understanding the problem.
|
|
|
|
|
|
|
|
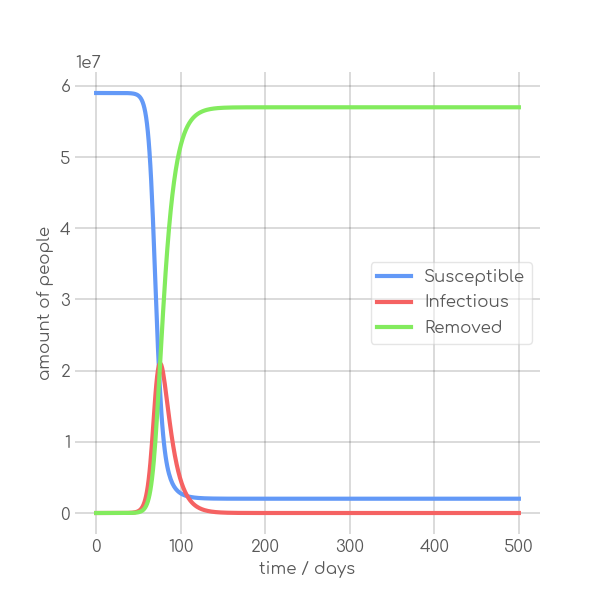
In 1927, Kermack and McKendrick~\cite{1927} introduced the \emph{SIR Model},
|
|
In 1927, Kermack and McKendrick~\cite{1927} introduced the \emph{SIR Model},
|
|
|
which subsequently became one of the most influential epidemiological models.
|
|
which subsequently became one of the most influential epidemiological models.
|
|
|
|
|
+This model enables the modeling of infections during epidemiological events such as pandemics.
|
|
|
The book \emph{Mathematical Models in Biology}~\cite{EdelsteinKeshet2005}
|
|
The book \emph{Mathematical Models in Biology}~\cite{EdelsteinKeshet2005}
|
|
|
reiterates the model and serves as the foundation for the following explanation
|
|
reiterates the model and serves as the foundation for the following explanation
|
|
|
of SIR models.\\
|
|
of SIR models.\\
|
|
|
|
|
|
|
|
-The SIR Model is capable of illustrating diseases, which are transferred through
|
|
|
|
|
|
|
+The SIR model is capable of illustrating diseases, which are transferred through
|
|
|
contact or proximity of an individual carrying the illness and a healthy
|
|
contact or proximity of an individual carrying the illness and a healthy
|
|
|
individual. This is possible due to the distinction between infected beings
|
|
individual. This is possible due to the distinction between infected beings
|
|
|
who are carriers of the disease and the part of the population, which is
|
|
who are carriers of the disease and the part of the population, which is
|
|
|
susceptible to infection. In the model, the mentioned groups are capable to
|
|
susceptible to infection. In the model, the mentioned groups are capable to
|
|
|
-change, by healthy individuals becoming infected. In the real world the size of
|
|
|
|
|
-a population is subject to a number of factors that can contribute to change.
|
|
|
|
|
|
|
+change, e.g., healthy individuals becoming infected. In the real world the size
|
|
|
|
|
+of a population is subject to a number of factors that can contribute to change.
|
|
|
The population is increased by the occurrence of births and decreased by the
|
|
The population is increased by the occurrence of births and decreased by the
|
|
|
occurrence of deaths. There are different reasons for mortality, including the
|
|
occurrence of deaths. There are different reasons for mortality, including the
|
|
|
natural aging process or the development of other diseases. To omit this factor
|
|
natural aging process or the development of other diseases. To omit this factor
|
|
|
of complexity, the model assumes the size $N$ of the population remains constant
|
|
of complexity, the model assumes the size $N$ of the population remains constant
|
|
|
throughout the duration of the epidemic. The population $N$ is comprised of
|
|
throughout the duration of the epidemic. The population $N$ is comprised of
|
|
|
three distinct groups: the \emph{susceptible} group $S$, the \emph{infectious}
|
|
three distinct groups: the \emph{susceptible} group $S$, the \emph{infectious}
|
|
|
-group $I$ and the \emph{removed} group $R$ (hence SIR Model). For $S$, $I$, $R$
|
|
|
|
|
|
|
+group $I$ and the \emph{removed} group $R$ (hence SIR model). For $S$, $I$, $R$
|
|
|
and $N$ applies:
|
|
and $N$ applies:
|
|
|
-\begin{equation}
|
|
|
|
|
|
|
+\begin{equation} \label{eq:N_char}
|
|
|
N = S + I + R.
|
|
N = S + I + R.
|
|
|
\end{equation}
|
|
\end{equation}
|
|
|
The model makes another assumption by stating that recovered people are immune
|
|
The model makes another assumption by stating that recovered people are immune
|
|
@@ -182,32 +183,32 @@ carry the disease.
|
|
|
\begin{figure}[h]
|
|
\begin{figure}[h]
|
|
|
\centering
|
|
\centering
|
|
|
\includegraphics[scale=0.3]{sir_graph.png}
|
|
\includegraphics[scale=0.3]{sir_graph.png}
|
|
|
- \caption{SIR Model}
|
|
|
|
|
|
|
+ \caption{A visualization of the SIR model, illustrating $N$ being split in the
|
|
|
|
|
+ three groups $S$, $I$ and $R$.}
|
|
|
\label{fig:sir_model}
|
|
\label{fig:sir_model}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
|
-As visualized in the Figure~\ref{fig:sir_model} the
|
|
|
|
|
-individuals may transition between groups based on rates. The transmission rate
|
|
|
|
|
-$\beta$ is responsible for individuals becoming infected, while the rate of
|
|
|
|
|
-removal or recovery rate $\alpha$ (also referred to as $\delta$ or $\nu$ in the
|
|
|
|
|
-literature) moves individuals from $I$ to $R$.\\
|
|
|
|
|
-
|
|
|
|
|
-In order to model the problem mathematically using a system of differential
|
|
|
|
|
-equations as we describe in Section~\ref{sec:differentialEq}, it is necessary to
|
|
|
|
|
-make an assumption serving as the foundation for the model. In their book,
|
|
|
|
|
-Edelstein-Keshet makes the following assumption: ``The rate of transmission of
|
|
|
|
|
-a microparasitic disease is proportional to the rate of encounter of susceptible
|
|
|
|
|
-and infective individuals modelled by the product
|
|
|
|
|
-($\beta S I$)''~\cite{EdelsteinKeshet2005}. Kermack and McKendrick~\cite{1927}
|
|
|
|
|
-thus propose the following set of differential equations:
|
|
|
|
|
-\begin{equation}
|
|
|
|
|
|
|
+As visualized in the~\Cref{fig:sir_model} the
|
|
|
|
|
+individuals may transition between groups based on transition rates. The
|
|
|
|
|
+transmission rate $\beta$ is responsible for individuals becoming infected,
|
|
|
|
|
+while the rate of removal or recovery rate $\alpha$ (also referred to as
|
|
|
|
|
+$\delta$ or $\nu$, e.g.,~\cite{EdelsteinKeshet2005,Millevoi2023}) moves
|
|
|
|
|
+individuals from $I$ to $R$.\\
|
|
|
|
|
+
|
|
|
|
|
+We can describe this problem mathematically using a system of differential
|
|
|
|
|
+equations (see ~\Cref{sec:differentialEq}). Thus, Kermack and
|
|
|
|
|
+McKendrick~\cite{1927} propose the following set of differential equations:
|
|
|
|
|
+\begin{equation}\label{eq:sir}
|
|
|
\begin{split}
|
|
\begin{split}
|
|
|
\frac{dS}{dt} &= -\beta S I,\\
|
|
\frac{dS}{dt} &= -\beta S I,\\
|
|
|
\frac{dI}{dt} &= \beta S I - \alpha I,\\
|
|
\frac{dI}{dt} &= \beta S I - \alpha I,\\
|
|
|
- \frac{dR}{dt} &= \alpha I.
|
|
|
|
|
|
|
+ \frac{dR}{dt} &= \alpha I,
|
|
|
\end{split}
|
|
\end{split}
|
|
|
\end{equation}
|
|
\end{equation}
|
|
|
-The system shows the change of size of the groups per time unit due to
|
|
|
|
|
-infections, recoveries, and deaths.\\
|
|
|
|
|
|
|
+This, according to Edelstein-Keshet, is based on the following assumption:
|
|
|
|
|
+``The rate of transmission of a microparasitic disease is proportional to the
|
|
|
|
|
+rate of encounter of susceptible and infective individuals modelled by the
|
|
|
|
|
+product ($\beta S I$)''~\cite{EdelsteinKeshet2005}. The system shows the change
|
|
|
|
|
+in size of the groups per time unit due to infections, recoveries, and deaths.\\
|
|
|
|
|
|
|
|
The term $\beta SI$ describes the rate of encounters of susceptible and infected
|
|
The term $\beta SI$ describes the rate of encounters of susceptible and infected
|
|
|
individuals. This term is dependent on the size of $S$ and $I$, thus Anderson
|
|
individuals. This term is dependent on the size of $S$ and $I$, thus Anderson
|
|
@@ -225,7 +226,7 @@ real world aspect.\\
|
|
|
The initial phase of a pandemic is characterized by the infection of a small
|
|
The initial phase of a pandemic is characterized by the infection of a small
|
|
|
number of individuals, while the majority of the population remains susceptible.
|
|
number of individuals, while the majority of the population remains susceptible.
|
|
|
The infectious group has not yet infected any individuals thus
|
|
The infectious group has not yet infected any individuals thus
|
|
|
-neither recovery nor mortality is possible. Let $I_0\in\mathbb{N}_{\geq0}$ be
|
|
|
|
|
|
|
+neither recovery nor mortality is possible. Let $I_0\in\mathbb{N}$ be
|
|
|
the number of infected individuals at the beginning of the disease. Then,
|
|
the number of infected individuals at the beginning of the disease. Then,
|
|
|
\begin{equation}
|
|
\begin{equation}
|
|
|
\begin{split}
|
|
\begin{split}
|
|
@@ -241,38 +242,38 @@ emerged.\\
|
|
|
\centering
|
|
\centering
|
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{synth_alpha_beta}
|
|
|
|
|
- \caption{Basic configuration, $\alpha=0.35$, $\beta=0.2$}
|
|
|
|
|
|
|
+ \includegraphics[width=\textwidth]{reference_params_synth.png}
|
|
|
|
|
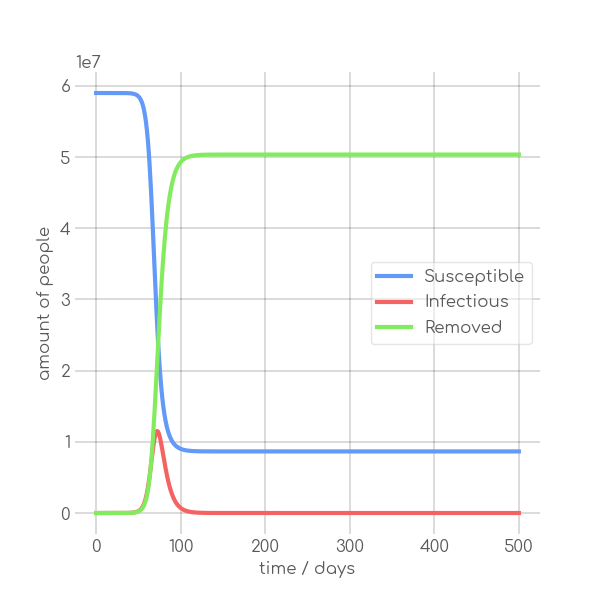
+ \caption{Basic configuration, $\alpha=0.35$, $\beta=0.5$}
|
|
|
\label{fig:synth_norm}
|
|
\label{fig:synth_norm}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
\hfill
|
|
\hfill
|
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{synth_alpha_high_beta}
|
|
|
|
|
- \caption{High $\alpha$ configuration, $\alpha=0.45$, $\beta=0.2$}
|
|
|
|
|
|
|
+ \includegraphics[width=\textwidth]{high_beta_synth.png}
|
|
|
|
|
+ \caption{High $\alpha$ configuration, $\alpha=0.45$, $\beta=0.5$}
|
|
|
\label{fig:synth_high_beta}
|
|
\label{fig:synth_high_beta}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
\hfill
|
|
\hfill
|
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
\begin{subfigure}[h]{0.3\textwidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{synth_alpha_low_beta}
|
|
|
|
|
- \caption{Low $\alpha$ configuration, $\alpha=0.25$, $\beta=0.2$}
|
|
|
|
|
|
|
+ \includegraphics[width=\textwidth]{low_beta_synth.png}
|
|
|
|
|
+ \caption{Low $\alpha$ configuration, $\alpha=0.25$, $\beta=0.5$}
|
|
|
\label{fig:synth_low_beta}
|
|
\label{fig:synth_low_beta}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
\hfill
|
|
\hfill
|
|
|
\begin{subfigure}[b]{0.3\textwidth}
|
|
\begin{subfigure}[b]{0.3\textwidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{synth_high_alpha_beta}
|
|
|
|
|
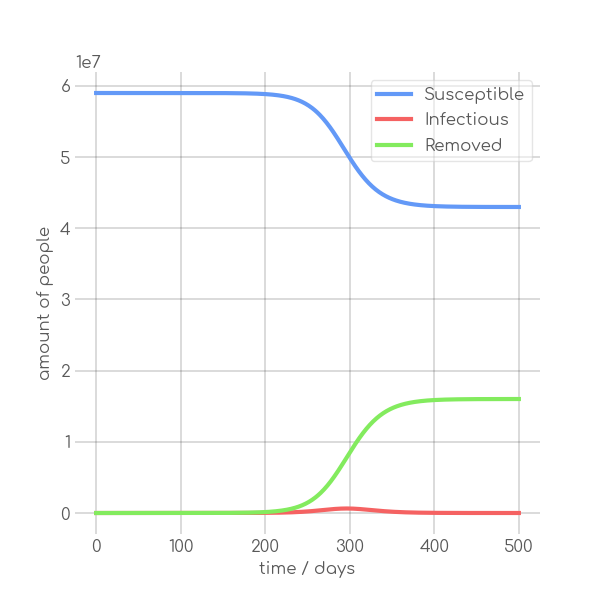
- \caption{High $\beta$ configuration, $\alpha=0.35$, $\beta=0.3$}
|
|
|
|
|
|
|
+ \includegraphics[width=\textwidth]{high_alpha_synth.png}
|
|
|
|
|
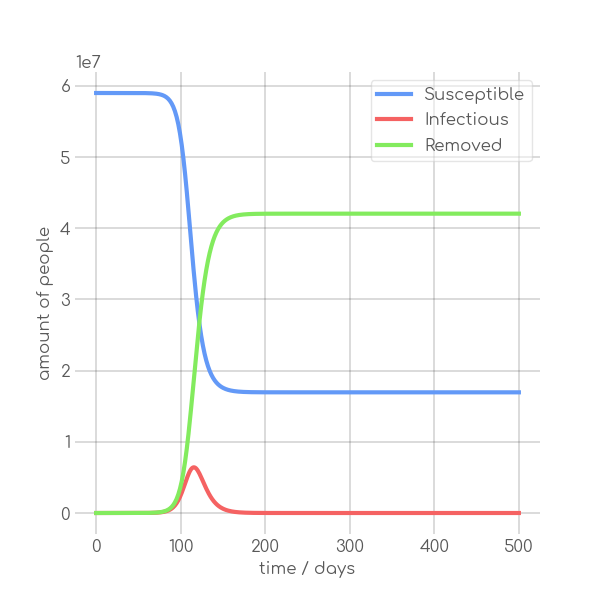
+ \caption{High $\beta$ configuration, $\alpha=0.35$, $\beta=0.6$}
|
|
|
\label{fig:synth_high_alpha}
|
|
\label{fig:synth_high_alpha}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
\begin{subfigure}[b]{0.3\textwidth}
|
|
\begin{subfigure}[b]{0.3\textwidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{synth_low_alpha_beta}
|
|
|
|
|
- \caption{Low $\beta$ configuration, $\alpha=0.35$, $\beta=0.1$}
|
|
|
|
|
|
|
+ \includegraphics[width=\textwidth]{low_alpha_synth.png}
|
|
|
|
|
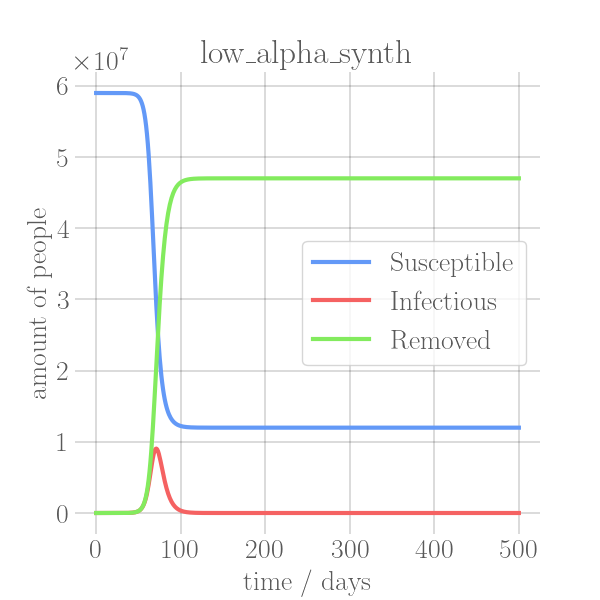
+ \caption{Low $\beta$ configuration, $\alpha=0.35$, $\beta=0.3$}
|
|
|
\label{fig:synth_low_alpha}
|
|
\label{fig:synth_low_alpha}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
- \caption{Synthetic data, using the Equations~\ref{eq:modSIR} and $N=7.9\cdot 10^6$,
|
|
|
|
|
|
|
+ \caption{Synthetic data, using~\Cref{eq:modSIR} and $N=7.9\cdot 10^6$,
|
|
|
$I_0=10$ with different sets of parameters.}
|
|
$I_0=10$ with different sets of parameters.}
|
|
|
\label{fig:synth_sir}
|
|
\label{fig:synth_sir}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
@@ -280,24 +281,97 @@ emerged.\\
|
|
|
In the SIR model the temporal occurrence and the height of the peak (or peaks)
|
|
In the SIR model the temporal occurrence and the height of the peak (or peaks)
|
|
|
of the infectious group are of paramount importance for understanding the
|
|
of the infectious group are of paramount importance for understanding the
|
|
|
dynamics of a pandemic. A low peak occurring at a late point in time indicates
|
|
dynamics of a pandemic. A low peak occurring at a late point in time indicates
|
|
|
-that the disease is unable to keep the pace with the rate of recovery, resulting
|
|
|
|
|
|
|
+that the disease is unable to keep pace with the rate of recovery, resulting
|
|
|
in its demise before it can exert a significant influence on the population. In
|
|
in its demise before it can exert a significant influence on the population. In
|
|
|
-contrast, an early, high peak means that the disease is rapidly transmitted
|
|
|
|
|
|
|
+contrast, an early and high peak means that the disease is rapidly transmitted
|
|
|
through the population, with a significant proportion of individuals having been
|
|
through the population, with a significant proportion of individuals having been
|
|
|
-infected. Figure~\ref{fig:sir_model} illustrates the impact of modifying either
|
|
|
|
|
-$\beta$ or $\alpha$ while simulating a pandemic using a model
|
|
|
|
|
-such as~\ref{eq:modSIR}. It is evident that both the transmission rate $\beta$
|
|
|
|
|
-and the recovery rate $\alpha$ influence the height and time of occurrence of
|
|
|
|
|
-the peak of $I$. When the number of infections exceeds the number of recoveries
|
|
|
|
|
-the peak of $I$ will occur early and will be high. On the other hand, if
|
|
|
|
|
-recoveries occur at a faster rate than new infections the peak will occur later
|
|
|
|
|
-and will be low. This means, that it is crucial to know both $\beta$ and
|
|
|
|
|
-$\alpha$ to be able to quantize a pandemic using the SIR model.
|
|
|
|
|
|
|
+infected.~\Cref{fig:sir_model} illustrates the impact of modifying either
|
|
|
|
|
+$\beta$ or $\alpha$ while simulating a pandemic using a model such
|
|
|
|
|
+as~\Cref{eq:modSIR}. It is evident that both the transmission rate $\beta$
|
|
|
|
|
+and the recovery rate $\alpha$ influence the height and time of the peak of $I$.
|
|
|
|
|
+When the number of infections exceeds the number of recoveries, the peak of $I$
|
|
|
|
|
+will occur early and will be high. On the other hand, if recoveries occur at a
|
|
|
|
|
+faster rate than new infections the peak will occur later and will be low. This
|
|
|
|
|
+means, that it is crucial to know both $\beta$ and $\alpha$ to be able to
|
|
|
|
|
+quantize a pandemic using the SIR model.
|
|
|
|
|
|
|
|
% -------------------------------------------------------------------
|
|
% -------------------------------------------------------------------
|
|
|
|
|
|
|
|
-\subsection{reduced SIR Model}
|
|
|
|
|
|
|
+\subsection{Reduced SIR Model and the Reproduction Number}
|
|
|
\label{sec:pandemicModel:rsir}
|
|
\label{sec:pandemicModel:rsir}
|
|
|
|
|
+The~\Cref{sec:pandemicModel:sir} presents the classical SIR model. The model
|
|
|
|
|
+comprises two parameters $\beta$ and $\alpha$, which describe the course of a
|
|
|
|
|
+pandemic over its duration. This is beneficial when examining the overall
|
|
|
|
|
+pandemic; however, in the real world, disease behavior is dynamic, and the
|
|
|
|
|
+values of the parameters $\beta$ and $\alpha$ change at each time point. The
|
|
|
|
|
+reason for this is due to events such as the implementation of countermeasures
|
|
|
|
|
+that reduce the contact between the infectious and susceptible individuals, the
|
|
|
|
|
+emergence of a new variant of the disease that increases its infectivity or
|
|
|
|
|
+deadliness, or the administration of a vaccination that provides previously
|
|
|
|
|
+susceptible individuals with immunity without ever being infectious. To address
|
|
|
|
|
+this Millevoi et al.~\cite{Millevoi2023} introduce a model that simultaneously
|
|
|
|
|
+reduces the size of the system of differential equations and solves the problem
|
|
|
|
|
+of time scaling at hand.\\
|
|
|
|
|
+
|
|
|
|
|
+First, they alter the definition of $\beta$ and $\alpha$ to be dependent on the time interval
|
|
|
|
|
+$\mathcal{T} = [t_0, t_f]\subseteq \mathbb{R}_{\geq0}$,
|
|
|
|
|
+\begin{equation}
|
|
|
|
|
+ \beta: \mathcal{T}\rightarrow\mathbb{R}_{\geq0}, \quad\alpha: \mathcal{T}\rightarrow\mathbb{R}_{\geq0}.
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+Another crucial element is $D(t) = \frac{1}{\alpha(t)}$, which represents the initial time
|
|
|
|
|
+span an infected individual requires to recuperate. Subsequently, at the initial time point
|
|
|
|
|
+$t_0$, the \emph{reproduction number},
|
|
|
|
|
+\begin{equation}
|
|
|
|
|
+ \RO = \beta(t_0)D(t_0) = \frac{\beta(t_0)}{\alpha(t_0)},
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+represents the number of susceptible individuals, that one infectious individual
|
|
|
|
|
+infects at the onset of the pandemic.In light of the effects of $\beta$ and
|
|
|
|
|
+$\alpha$ (see~\Cref{sec:pandemicModel:sir}), $\RO > 1$ indicates that the
|
|
|
|
|
+pandemic is emerging. In this scenario $\alpha$ is relatively low due to the
|
|
|
|
|
+limited number of infections resulting from $I(t_0) << S(t_0)$. When $\RO < 1$,
|
|
|
|
|
+the disease is spreading rapidly across the population, with an increase in $I$
|
|
|
|
|
+occurring at a high rate. Nevertheless, $\RO$ does not cover the entire time
|
|
|
|
|
+span. For this reason, Millevoi et al.~\cite{Millevoi2023} introduce $\Rt$
|
|
|
|
|
+which has the same interpretation as $\RO$, with the exception that $\Rt$ is
|
|
|
|
|
+dependent on time. The definition of the time-dependent reproduction number on
|
|
|
|
|
+the time interval $\mathcal{T}$ with the population size $N$,
|
|
|
|
|
+\begin{equation}\label{eq:repr_num}
|
|
|
|
|
+ \Rt=\frac{\beta(t)}{\alpha(t)}\cdot\frac{S(t)}{N}
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+includes the rates of change for information about the spread of the disease and
|
|
|
|
|
+information of the decrease of the ratio of susceptible individuals in the
|
|
|
|
|
+population. In contrast to $\beta$ and $\alpha$, $\Rt$ is not a parameter but
|
|
|
|
|
+a state variable in the model and enabling the following reduction of the SIR
|
|
|
|
|
+model.\\
|
|
|
|
|
+
|
|
|
|
|
+\Cref{eq:N_char} allows for the calculation of the value of the group $R$ using
|
|
|
|
|
+$S$ and $I$, with the term $R(t)=N-S(t)-I(t)$. Thus,
|
|
|
|
|
+\begin{equation}
|
|
|
|
|
+ \begin{split}
|
|
|
|
|
+ \frac{dS}{dt} &= \alpha(\Rt-1)I(t),\\
|
|
|
|
|
+ \frac{dI}{dt} &= -\alpha\Rt I(t),
|
|
|
|
|
+ \end{split}
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+is the reduction of~\Cref{eq:sir} on the time interval $\mathcal{T}$ using this
|
|
|
|
|
+characteristic and the reproduction number \Rt (see ~\Cref{eq:repr_num}).
|
|
|
|
|
+Another issue that Millevoi et al.~\cite{Millevoi2023} seek to address is the
|
|
|
|
|
+extensive range of values that the SIR groups can assume, spanning from $0$ to
|
|
|
|
|
+$10^7$. Accordingly, they initially scale the time interval $\mathcal{T}$ using
|
|
|
|
|
+its borders to calculate the scaled time $t_s = \frac{t - t_0}{t_f - t_0}\in
|
|
|
|
|
+ [0, 1]$. Subsequently, they calculate the scaled groups,
|
|
|
|
|
+\begin{equation}
|
|
|
|
|
+ S_s(t_s) = \frac{S(t)}{C},\quad I_s(t_s) = \frac{I(t)}{C},\quad R_s(t_s) = \frac{R(t)}{C},
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+using a large constant scaling factor $C\in\mathbb{N}$. Applying this to the
|
|
|
|
|
+variable $I$, results in,
|
|
|
|
|
+\begin{equation}
|
|
|
|
|
+ \frac{dI_s}{dt_s} = \alpha(t_f - t_0)(\Rt - 1)I_s(t_s),
|
|
|
|
|
+\end{equation}
|
|
|
|
|
+a further reduced version of~\Cref{eq:sir} results in a more streamlined and
|
|
|
|
|
+efficient process, as it entails the elimination of a parameter($\beta$) and two
|
|
|
|
|
+state variables ($S$ and $R$), while adding the state variable $\Rt$. This is a
|
|
|
|
|
+crucial aspect for the automated resolution of such differential equation
|
|
|
|
|
+systems, as we describe in~\Cref{sec:mlp}.
|
|
|
|
|
|
|
|
% -------------------------------------------------------------------
|
|
% -------------------------------------------------------------------
|
|
|
|
|
|