|
|
@@ -1,3 +1,6 @@
|
|
|
+title: libigl Tutorial
|
|
|
+author: Alec Jacobson, Daniele Pannozo and others
|
|
|
+date: 20 June 2014
|
|
|
css: style.css
|
|
|
html header: <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
|
|
|
<link rel="stylesheet" href="http://yandex.st/highlightjs/7.3/styles/default.min.css">
|
|
|
@@ -5,8 +8,25 @@ html header: <script type="text/javascript" src="http://cdn.mathjax.org/mathja
|
|
|
<script>hljs.initHighlightingOnLoad();</script>
|
|
|
|
|
|
# Introduction
|
|
|
-
|
|
|
-TODO
|
|
|
+Libigl is an open source C++ library for geometry processing research and
|
|
|
+development.
|
|
|
+Dropping the heavy data structures of tradition geometry libraries, libigl is
|
|
|
+a simple header-only library of encapsulated functions.
|
|
|
+%
|
|
|
+This combines the rapid prototyping familiar to \textsc{Matlab} or
|
|
|
+\textsc{Python} programmers
|
|
|
+with the performance and versatility of C++.
|
|
|
+%
|
|
|
+The tutorial is a self-contained, hands-on introduction to \libigl.
|
|
|
+%
|
|
|
+Via live coding and interactive examples, we demonstrate how to accomplish
|
|
|
+various common geometry processing tasks such as computation of differential
|
|
|
+quantities and operators, real-time deformation, global parametrization,
|
|
|
+numerical optimization and mesh repair.
|
|
|
+%
|
|
|
+Accompanying lecture notes contain further details and cross-platform example
|
|
|
+applications for each topic.
|
|
|
+\end{abstract}
|
|
|
|
|
|
# Index
|
|
|
|
|
|
@@ -14,6 +34,8 @@ TODO
|
|
|
* **101_Serialization**: Example of using the XML serialization framework
|
|
|
* **102_DrawMesh**: Example of plotting a mesh
|
|
|
* [202 Gaussian Curvature](#gaus)
|
|
|
+* [203 Curvature Directions](#curv)
|
|
|
+* [204 Gradient](#grad)
|
|
|
|
|
|
# Compilation Instructions
|
|
|
|
|
|
@@ -68,7 +90,7 @@ on a triangle mesh is via a vertex's _angular deficit_:
|
|
|
$k_G(v_i) = 2π - \sum\limits_{j\in N(i)}θ_{ij},$
|
|
|
|
|
|
where $N(i)$ are the triangles incident on vertex $i$ and $θ_{ij}$ is the angle
|
|
|
-at vertex $i$ in triangle $j$. (**Alec: cite Meyer or something**)
|
|
|
+at vertex $i$ in triangle $j$ [][#meyer_2003].
|
|
|
|
|
|
Just like the continuous analog, our discrete Gaussian curvature reveals
|
|
|
elliptic, hyperbolic and parabolic vertices on the domain.
|
|
|
@@ -76,7 +98,7 @@ elliptic, hyperbolic and parabolic vertices on the domain.
|
|
|

|
|
|
|
|
|
-## <a id=principal></a> Curvature Directions
|
|
|
+## <a id=curv></a> Curvature Directions
|
|
|
The two principal curvatures $(k_1,k_2)$ at a point on a surface measure how much the
|
|
|
surface bends in different directions. The directions of maximum and minimum
|
|
|
(signed) bending are call principal directions and are always
|
|
|
@@ -93,7 +115,7 @@ normal:
|
|
|
$-\Delta \mathbf{x} = H \mathbf{n}.$
|
|
|
|
|
|
It is easy to compute this on a discrete triangle mesh in libigl using the cotangent
|
|
|
-Laplace-Beltrami operator (**Alec: cite Meyer**):
|
|
|
+Laplace-Beltrami operator [][#meyer_2003].
|
|
|
|
|
|
```cpp
|
|
|
#include <igl/cotmatrix.h>
|
|
|
@@ -111,10 +133,10 @@ H = (HN.rowwise().squaredNorm()).array().sqrt();
|
|
|
|
|
|
Combined with the angle defect definition of discrete Gaussian curvature, one
|
|
|
can define principal curvatures and use least squares fitting to find
|
|
|
-directions (**Alec: cite meyer**).
|
|
|
+directions [][#meyer_2003].
|
|
|
|
|
|
Alternatively, a robust method for determining principal curvatures is via
|
|
|
-quadric fitting (**Alec: cite whatever we're using**). In the neighborhood
|
|
|
+quadric fitting [][#pannozo_2010]. In the neighborhood
|
|
|
around every vertex, a best-fit quadric is found and principal curvature values
|
|
|
and directions are sampled from this quadric. With these in tow, one can
|
|
|
compute mean curvature and Gaussian curvature as sums and products
|
|
|
@@ -133,3 +155,48 @@ int main(int argc, char * argv[])
|
|
|
return 0;
|
|
|
}
|
|
|
```
|
|
|
+
|
|
|
+## <a id=grad></a> Gradient
|
|
|
+Scalar functions on a surface can be discretized as a piecewise linear function
|
|
|
+with values defined at each mesh vertex:
|
|
|
+
|
|
|
+ $f(\mathbf{x}) \approx \sum\limits_{i=0}^n \phi_i(\mathbf{x})\, f_i,$
|
|
|
+
|
|
|
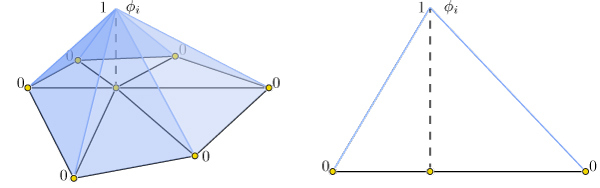
+where $\phi_i$ is a piecewise linear hat function defined by the mesh so that
|
|
|
+for each triangle $\phi_i$ is _the_ linear function which is one only at
|
|
|
+vertex $i$ and zero at the other corners.
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+Thus gradients of such piecewise linear functions are simply sums of gradients
|
|
|
+of the hat functions:
|
|
|
+
|
|
|
+ $\nabla f(\mathbf{x}) \approx
|
|
|
+ \nabla \sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i =
|
|
|
+ \sum\limits_{i=0}^n \nabla \phi_i(\mathbf{x})\, f_i.$
|
|
|
+
|
|
|
+This reveals that the gradient is a linear function of the vector of $f_i$
|
|
|
+values. Because $\phi_i$ are linear in each triangle their gradient are
|
|
|
+_constant_ in each triangle. Thus our discrete gradient operator can be written
|
|
|
+as a matrix multiplication taking vertex values to triangle values:
|
|
|
+
|
|
|
+ $\nabla f \approx \mathbf{G}\,\mathbf{f},$
|
|
|
+
|
|
|
+where $\mathbf{f}$ is $n\times 1$ and $\mathbf{G}$ is an $m\times n$ sparse
|
|
|
+matrix. This matrix $\mathbf{G}$ can be derived geometrically, e.g.
|
|
|
+[ch. 2][#jacobson_thesis_2013].
|
|
|
+Libigl's `gradMat`**Alec: check name** function computes $\mathbf{G}$ for
|
|
|
+triangle and tetrahedral meshes:
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+[#meyer_2003]: Mark Meyer and Mathieu Desbrun and Peter Schröder and Alan H. Barr,
|
|
|
+"Discrete Differential-Geometry Operators for Triangulated
|
|
|
+2-Manifolds," 2003.
|
|
|
+[#pannozo_2010]: Daniele Pannozo, Enrico Puppo, Luigi Rocca,
|
|
|
+"Efficient Multi-scale Curvature and Crease Estimation," 2010.
|
|
|
+[#jacobson_thesis_2013]: Alec Jacobson,
|
|
|
+_Algorithms and Interfaces for Real-Time Deformation of 2D and 3D Shapes_,
|
|
|
+2013.
|