add reduced sir section and corrected sir section

chapters/chap02/chap02.tex

@@ -11,16 +11,16 @@
 \label{chap:background}
 
 This chapter introduces the theoretical knowledge that forms the foundation of
-the work presented in this thesis. In Sections~\ref{sec:domain}
-and~\ref{sec:differentialEq}, we talk about differential equations and the
+the work presented in this thesis. In~\Cref{sec:domain}
+and~\Cref{sec:differentialEq}, we talk about differential equations and the
 underlying theory. In these Sections both the explanations and the approach are
 strongly based on the book on analysis by Rudin~\cite{Rudin2007} and the book
 about ordinary differential equations by Tenenbaum and
 Pollard~\cite{Tenenbaum1985}. Subsequently, we employ this knowledge to examine
-various pandemic models in Section~\ref{sec:epidemModel}.
+various pandemic models in~\Cref{sec:epidemModel}.
 Finally, we address the topic of neural networks with a focus on the multilayer
-perceptron in Section~\ref{sec:mlp} and physics informed neural networks in
-Section~\ref{sec:pinn}.
+perceptron in~\Cref{sec:mlp} and physics informed neural networks
+in~\Cref{sec:pinn}.
 
 % -------------------------------------------------------------------
 
@@ -109,7 +109,7 @@ Then, Newton's second law translates mathematically to
 It is evident that the acceleration, $a=\frac{dv}{dt}$, as the rate of change of
 the velocity is part of the equation. Additionally, the velocity of a body is
 the derivative of the distance traveled by that body. Based on these findings,
-we can rewrite the equation~\ref{eq:newtonSecLaw} to
+we can rewrite the~\Cref{eq:newtonSecLaw} to
 \begin{equation}
   F=ma=m\frac{d^2s}{dt^2}.
 \end{equation}\\
@@ -153,26 +153,27 @@ and relations that are pivotal to understanding the problem.
 
 In 1927, Kermack and McKendrick~\cite{1927} introduced the \emph{SIR Model},
 which subsequently became one of the most influential epidemiological models.
+This model enables the modeling of infections during epidemiological events such as pandemics.
 The book \emph{Mathematical Models in Biology}~\cite{EdelsteinKeshet2005}
 reiterates the model and serves as the foundation for the following explanation
 of SIR models.\\
 
-The SIR Model is capable of illustrating diseases, which are transferred through
+The SIR model is capable of illustrating diseases, which are transferred through
 contact or proximity of an individual carrying the illness and a healthy
 individual. This is possible due to the distinction between infected beings
 who are carriers of the disease and the part of the population, which is
 susceptible to infection. In the model, the mentioned groups are capable to
-change, by healthy individuals becoming infected. In the real world the size of
-a population is subject to a number of factors that can contribute to change.
+change, e.g.,  healthy individuals becoming infected. In the real world the size
+of a population is subject to a number of factors that can contribute to change.
 The population is increased by the occurrence of births and decreased by the
 occurrence of deaths. There are different reasons for mortality, including the
 natural aging process or the development of other diseases. To omit this factor
 of complexity, the model assumes the size $N$ of the population remains constant
 throughout the duration of the epidemic. The population $N$ is comprised of
 three distinct groups: the \emph{susceptible} group $S$, the \emph{infectious}
-group $I$ and the \emph{removed} group $R$ (hence SIR Model). For $S$, $I$, $R$
+group $I$ and the \emph{removed} group $R$ (hence SIR model). For $S$, $I$, $R$
 and $N$ applies:
-\begin{equation}
+\begin{equation} \label{eq:N_char}
   N = S + I + R.
 \end{equation}
 The model makes another assumption by stating that recovered people are immune
@@ -182,32 +183,32 @@ carry the disease.
 \begin{figure}[h]
   \centering
   \includegraphics[scale=0.3]{sir_graph.png}
-  \caption{SIR Model}
+  \caption{A visualization of the SIR model, illustrating $N$ being split in the
+    three groups $S$, $I$ and $R$.}
   \label{fig:sir_model}
 \end{figure}
-As visualized in the Figure~\ref{fig:sir_model} the
-individuals may transition between groups based on rates. The transmission rate
-$\beta$ is responsible for individuals becoming infected, while the rate of
-removal or recovery rate $\alpha$ (also referred to as $\delta$ or $\nu$ in the
-literature) moves individuals from $I$ to $R$.\\
-
-In order to model the problem mathematically using a system of differential
-equations as we describe in Section~\ref{sec:differentialEq}, it is necessary to
-make an assumption serving as the foundation for the model. In their book,
-Edelstein-Keshet makes the following assumption: ``The rate of transmission of
-a microparasitic disease is proportional to the rate of encounter of susceptible
-and infective individuals modelled by the product
-($\beta S I$)''~\cite{EdelsteinKeshet2005}. Kermack and McKendrick~\cite{1927}
-thus propose the following set of differential equations:
-\begin{equation}
+As visualized in the~\Cref{fig:sir_model} the
+individuals may transition between groups based on transition rates. The
+transmission rate $\beta$ is responsible for individuals becoming infected,
+while the rate of removal or recovery rate $\alpha$ (also referred to as
+$\delta$ or $\nu$, e.g.,~\cite{EdelsteinKeshet2005,Millevoi2023}) moves
+individuals from $I$ to $R$.\\
+
+We can describe this problem mathematically using a system of differential
+equations (see ~\Cref{sec:differentialEq}). Thus, Kermack and
+McKendrick~\cite{1927} propose the following set of differential equations:
+\begin{equation}\label{eq:sir}
   \begin{split}
     \frac{dS}{dt} &= -\beta S I,\\
     \frac{dI}{dt} &= \beta S I - \alpha I,\\
-    \frac{dR}{dt} &= \alpha I.
+    \frac{dR}{dt} &= \alpha I,
   \end{split}
 \end{equation}
-The system shows the change of size of the groups per time unit due to
-infections, recoveries, and deaths.\\
+This, according to Edelstein-Keshet, is based on the following assumption:
+``The rate of transmission of a microparasitic disease is proportional to the
+rate of encounter of susceptible and infective individuals modelled by the
+product ($\beta S I$)''~\cite{EdelsteinKeshet2005}. The system shows the change
+in size of the groups per time unit due to infections, recoveries, and deaths.\\
 
 The term $\beta SI$ describes the rate of encounters of susceptible and infected
 individuals. This term is dependent on the size of $S$ and $I$, thus Anderson
@@ -225,7 +226,7 @@ real world aspect.\\
 The initial phase of a pandemic is characterized by the infection of a small
 number of individuals, while the majority of the population remains susceptible.
 The infectious group has not yet infected any individuals thus
-neither recovery nor mortality is possible. Let $I_0\in\mathbb{N}_{\geq0}$ be
+neither recovery nor mortality is possible. Let $I_0\in\mathbb{N}$ be
 the number of infected individuals at the beginning of the disease. Then,
 \begin{equation}
   \begin{split}
@@ -241,38 +242,38 @@ emerged.\\
   \centering
   \begin{subfigure}[h]{0.3\textwidth}
     \centering
-    \includegraphics[width=\textwidth]{synth_alpha_beta}
-    \caption{Basic configuration, $\alpha=0.35$, $\beta=0.2$}
+    \includegraphics[width=\textwidth]{reference_params_synth.png}
+    \caption{Basic configuration, $\alpha=0.35$, $\beta=0.5$}
     \label{fig:synth_norm}
   \end{subfigure}
   \hfill
   \begin{subfigure}[h]{0.3\textwidth}
     \centering
-    \includegraphics[width=\textwidth]{synth_alpha_high_beta}
-    \caption{High $\alpha$ configuration, $\alpha=0.45$, $\beta=0.2$}
+    \includegraphics[width=\textwidth]{high_beta_synth.png}
+    \caption{High $\alpha$ configuration, $\alpha=0.45$, $\beta=0.5$}
     \label{fig:synth_high_beta}
   \end{subfigure}
   \hfill
   \begin{subfigure}[h]{0.3\textwidth}
     \centering
-    \includegraphics[width=\textwidth]{synth_alpha_low_beta}
-    \caption{Low $\alpha$ configuration, $\alpha=0.25$, $\beta=0.2$}
+    \includegraphics[width=\textwidth]{low_beta_synth.png}
+    \caption{Low $\alpha$ configuration, $\alpha=0.25$, $\beta=0.5$}
     \label{fig:synth_low_beta}
   \end{subfigure}
   \hfill
   \begin{subfigure}[b]{0.3\textwidth}
     \centering
-    \includegraphics[width=\textwidth]{synth_high_alpha_beta}
-    \caption{High $\beta$ configuration, $\alpha=0.35$, $\beta=0.3$}
+    \includegraphics[width=\textwidth]{high_alpha_synth.png}
+    \caption{High $\beta$ configuration, $\alpha=0.35$, $\beta=0.6$}
     \label{fig:synth_high_alpha}
   \end{subfigure}
   \begin{subfigure}[b]{0.3\textwidth}
     \centering
-    \includegraphics[width=\textwidth]{synth_low_alpha_beta}
-    \caption{Low $\beta$ configuration, $\alpha=0.35$, $\beta=0.1$}
+    \includegraphics[width=\textwidth]{low_alpha_synth.png}
+    \caption{Low $\beta$ configuration, $\alpha=0.35$, $\beta=0.3$}
     \label{fig:synth_low_alpha}
   \end{subfigure}
-  \caption{Synthetic data, using the Equations~\ref{eq:modSIR} and $N=7.9\cdot 10^6$,
+  \caption{Synthetic data, using~\Cref{eq:modSIR} and $N=7.9\cdot 10^6$,
     $I_0=10$ with different sets of parameters.}
   \label{fig:synth_sir}
 \end{figure}
@@ -280,24 +281,97 @@ emerged.\\
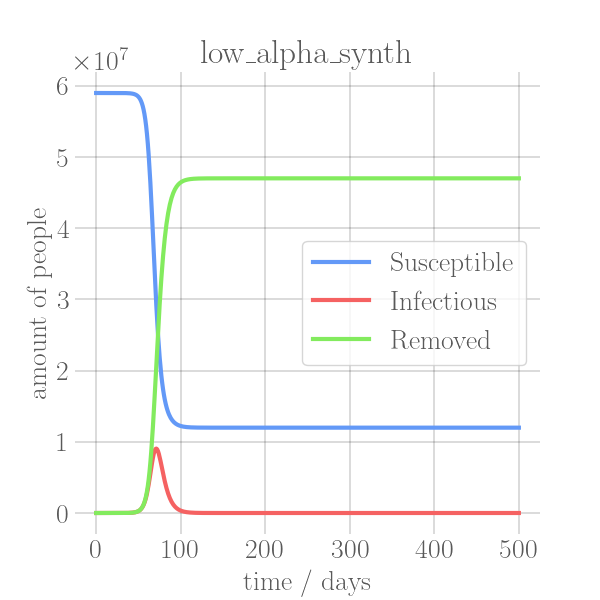
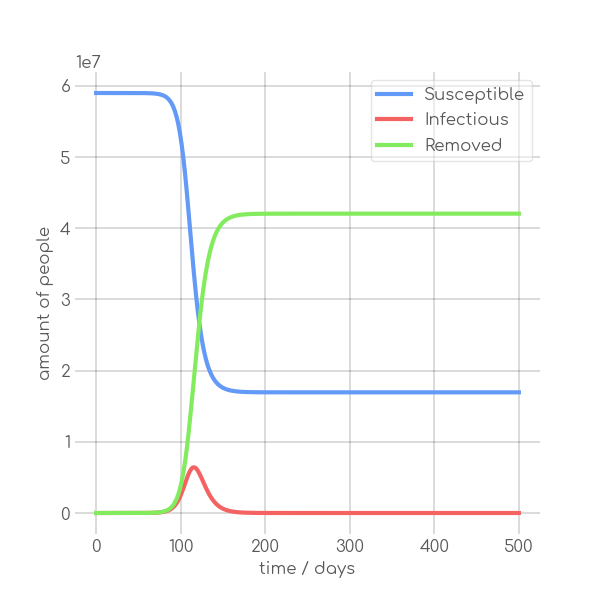
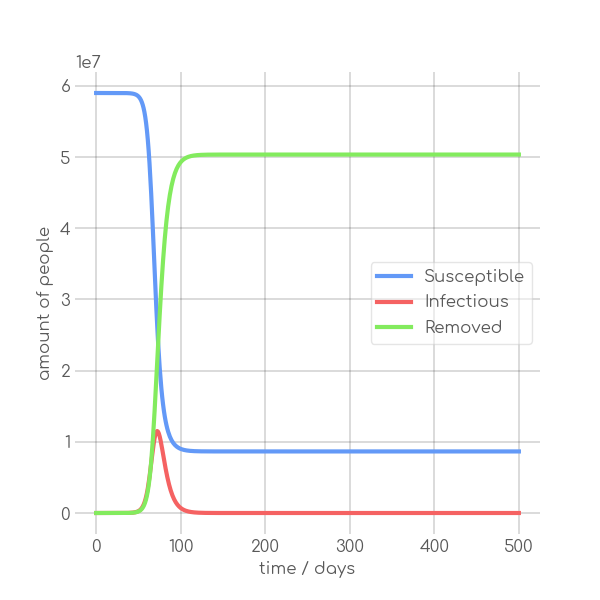
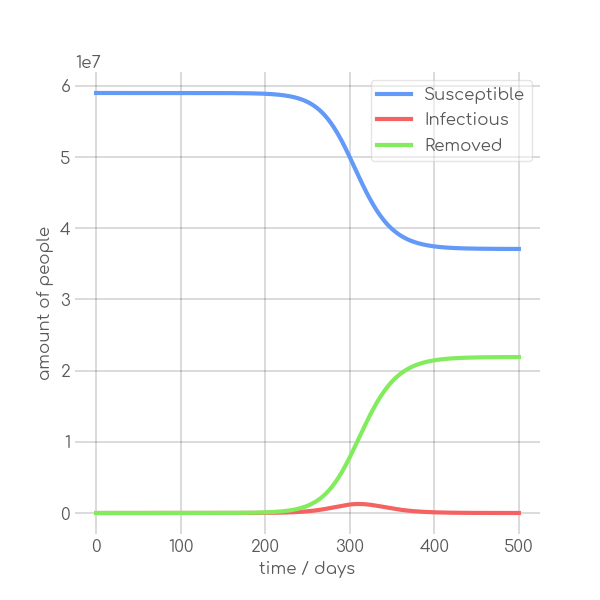
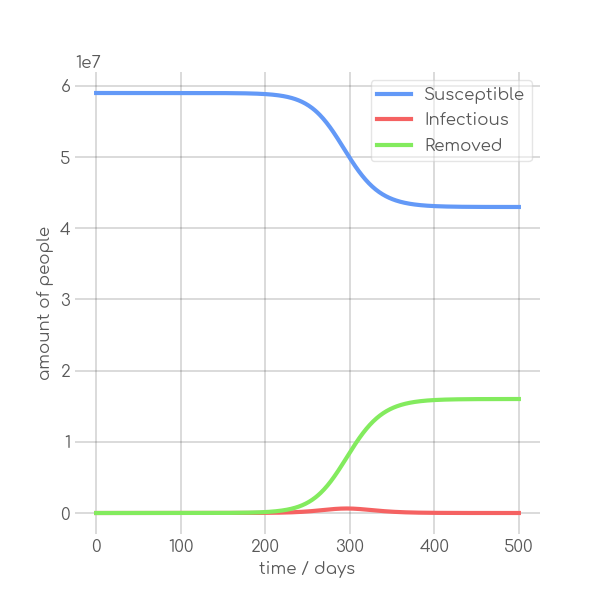
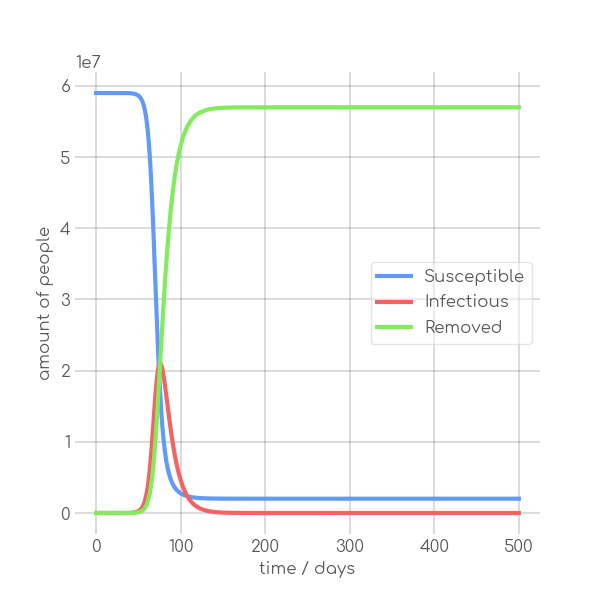
 In the SIR model the temporal occurrence and the height of the peak (or peaks)
 of  the infectious group are of paramount importance for understanding the
 dynamics of a pandemic. A low peak occurring at a late point in time indicates
-that the disease is unable to keep the pace with the rate of recovery, resulting
+that the disease is unable to keep pace with the rate of recovery, resulting
 in its demise before it can exert a significant influence on the population. In
-contrast, an early, high peak means that the disease is rapidly transmitted
+contrast, an early and high peak means that the disease is rapidly transmitted
 through the population, with a significant proportion of individuals having been
-infected. Figure~\ref{fig:sir_model} illustrates the impact of modifying either
-$\beta$ or $\alpha$ while simulating  a pandemic using a model
-such as~\ref{eq:modSIR}. It is evident that both the transmission rate $\beta$
-and the recovery rate $\alpha$ influence the height and time of occurrence of
-the peak of $I$. When the number of infections exceeds the number of recoveries
-the peak of $I$ will occur early and will be high. On the other hand, if
-recoveries occur at a faster rate than new infections the peak will occur later
-and will be low. This means, that it is crucial to know both $\beta$ and
-$\alpha$ to be able to quantize a pandemic using the SIR model.
+infected.~\Cref{fig:sir_model} illustrates the impact of modifying either
+$\beta$ or $\alpha$ while simulating  a pandemic using a model such
+as~\Cref{eq:modSIR}. It is evident that both the transmission rate $\beta$
+and the recovery rate $\alpha$ influence the height and time of the peak of $I$.
+When the number of infections exceeds the number of recoveries, the peak of $I$
+will occur early and will be high. On the other hand, if recoveries occur at a
+faster rate than new infections the peak will occur later and will be low. This
+means, that it is crucial to know both $\beta$ and $\alpha$ to be able to
+quantize a pandemic using the SIR model.
 
 % -------------------------------------------------------------------
 
-\subsection{reduced SIR Model}
+\subsection{Reduced SIR Model and the Reproduction Number}
 \label{sec:pandemicModel:rsir}
+The~\Cref{sec:pandemicModel:sir} presents the classical SIR model. The model
+comprises two parameters $\beta$ and $\alpha$, which describe the course of a
+pandemic over its duration. This is beneficial when examining the overall
+pandemic; however, in the real world, disease behavior is dynamic, and the
+values of the parameters $\beta$ and $\alpha$ change at each time point. The
+reason for this is due to events such as the implementation of countermeasures
+that reduce the contact between the infectious and susceptible individuals, the
+emergence of a new variant of the disease that increases its infectivity or
+deadliness, or the administration of a vaccination that provides previously
+susceptible individuals with immunity without ever being infectious. To address
+this Millevoi et al.~\cite{Millevoi2023} introduce a model that simultaneously
+reduces the size of the system of differential equations and solves the problem
+of time scaling at hand.\\
+
+First, they alter the definition of $\beta$ and $\alpha$ to be dependent on the time interval
+$\mathcal{T} = [t_0, t_f]\subseteq \mathbb{R}_{\geq0}$,
+\begin{equation}
+  \beta: \mathcal{T}\rightarrow\mathbb{R}_{\geq0}, \quad\alpha: \mathcal{T}\rightarrow\mathbb{R}_{\geq0}.
+\end{equation}
+Another crucial element is $D(t) = \frac{1}{\alpha(t)}$, which represents the initial time
+span an infected individual requires to recuperate. Subsequently, at the initial time point
+$t_0$, the \emph{reproduction number},
+\begin{equation}
+  \RO = \beta(t_0)D(t_0) = \frac{\beta(t_0)}{\alpha(t_0)},
+\end{equation}
+represents the number of susceptible individuals, that one infectious individual
+infects at the onset of the pandemic.In light of the effects of $\beta$ and
+$\alpha$ (see~\Cref{sec:pandemicModel:sir}), $\RO > 1$ indicates that the
+pandemic is emerging. In this scenario $\alpha$ is relatively low due to the
+limited number of infections resulting from $I(t_0) << S(t_0)$. When $\RO < 1$,
+the disease is spreading rapidly across the population, with an increase in $I$
+occurring at a high rate. Nevertheless, $\RO$ does not cover the entire time
+span. For this reason, Millevoi et al.~\cite{Millevoi2023} introduce $\Rt$
+which has the same interpretation as $\RO$, with the exception that $\Rt$ is
+dependent on time. The definition of the time-dependent reproduction number on
+the time interval $\mathcal{T}$ with the population size $N$,
+\begin{equation}\label{eq:repr_num}
+  \Rt=\frac{\beta(t)}{\alpha(t)}\cdot\frac{S(t)}{N}
+\end{equation}
+includes the rates of change for information about the spread of the disease and
+information of the decrease of the ratio of susceptible individuals in the
+population. In contrast to $\beta$ and $\alpha$, $\Rt$ is not a parameter but
+a state variable in the model and enabling the following reduction of the SIR
+model.\\
+
+\Cref{eq:N_char} allows for the calculation of the value of the group $R$ using
+$S$ and $I$, with the term $R(t)=N-S(t)-I(t)$. Thus,
+\begin{equation}
+  \begin{split}
+    \frac{dS}{dt} &= \alpha(\Rt-1)I(t),\\
+    \frac{dI}{dt} &= -\alpha\Rt I(t),
+  \end{split}
+\end{equation}
+is the reduction of~\Cref{eq:sir} on the time interval $\mathcal{T}$ using this
+characteristic and the reproduction number \Rt (see ~\Cref{eq:repr_num}).
+Another issue that Millevoi et al.~\cite{Millevoi2023} seek to address is the
+extensive range of values that the SIR groups can assume, spanning from $0$ to
+$10^7$. Accordingly, they initially scale the time interval $\mathcal{T}$ using
+its borders to calculate the scaled time $t_s = \frac{t - t_0}{t_f - t_0}\in
+  [0, 1]$. Subsequently, they calculate the scaled groups,
+\begin{equation}
+  S_s(t_s) = \frac{S(t)}{C},\quad I_s(t_s) = \frac{I(t)}{C},\quad R_s(t_s) = \frac{R(t)}{C},
+\end{equation}
+using a large constant scaling factor $C\in\mathbb{N}$. Applying this to the
+variable $I$, results in,
+\begin{equation}
+  \frac{dI_s}{dt_s} = \alpha(t_f - t_0)(\Rt - 1)I_s(t_s),
+\end{equation}
+a further reduced version of~\Cref{eq:sir} results in a more streamlined and
+efficient process, as it entails the elimination of a parameter($\beta$) and two
+state variables ($S$ and $R$), while adding the state variable $\Rt$. This is a
+crucial aspect for the automated resolution of such differential equation
+systems, as we describe in~\Cref{sec:mlp}.
 
 % -------------------------------------------------------------------
 

thesis.tex

@@ -26,6 +26,9 @@
 
 \begin{document}
 
+\newcommand{\RO}{\ensuremath{\mathcal{R}_0}}
+\newcommand{\Rt}{\ensuremath{\mathcal{R}_t}}
+
 \pagenumbering{Roman}
 
 \begin{dbvthesisTitlepageAndDeclaration}